Vektorer i koordinatsystemet

Innhold

17. Vektorer i koordinatsystemet#

Læringsmål

Kunne beskrive posisjonen til punkter i et koordinatsystem med vektorer
Kunne beskrive vektorer mellom to punkter i et koordinatsystem
Kunne bruke vektorer til å beskrive linjer i et koordinatsystem ved hjelp av parameterframstillinger og uttrykke parameterframstillinger som likninger og som vektorfunksjoner.

Vi har så langt introdusert vektorer som geometriske piler som har både retning og lengde. Vi etablerte at det ikke spiller noen rolle hvilket startpunkt de har for at de skal være like. Denne ideen med forflytning fra et startpunkt kan vi bruke til å beskrive ulike steder i et koordinatsystem. Vi er ofte interessert i å bruke vektorer til å beskrive

Posisjonen til punkter i et koordinatsystem
Vektorer mellom to punkter i et koordinatsystem

Vi skal bruke dette kapittelet på å utforske hvordan vi bruker vektorer til å beskrive posisjoner, vektorer mellom to punkter og utvide dette til å beskrive linjer i et koordinatsystem.

Posisjonsvektorer#

Når vi bruker en vektor til å beskrive posisjonen til et punkt \(P\) i et koordinatsystem, ser vi på vektoren som en pil som peker fra origo \(O\) til et punkt \(P\). Da skriver vi vektoren som \(\overrightarrow{OP}\) for å understreke at vektoren er en posisjonsvektor som starter i origo og peker ut til punktet \(P\) i koordinatsystemet.

Posisjonsvektorer

Når en vektor starter i origo \(O(0, 0)\) og peker ut til et punkt \(P(x, y)\) i et koordinatsystem, kaller vi vektoren for \(\lvec{OP}\) og sier at det er en posisjonsvektor som beskriver posisjonen til punktet \(P\) i koordinatssystemet.

Vektorkoordinatene til posisjonsvektoren er da gitt ved

\[ \lvec{OP} = [x, y] \]

der \(x\) og \(y\) er koordinatene til punktet \(P\).

Eksempel 1

To punkter er gitt ved \(A(2, 3)\) og \(B(3, -1)\).

Bestem posisjonsvektorene til punktene \(A\) og \(B\).

Løsning

Posisjonsvektorene er gitt ved de samme koordinatene som punktene har:

\[ \lvec{OA} = [2, 3] \qog \lvec{OB} = [3, -1] \]

Vektorene peker da ut til posisjonen punktene har i koordinatsystemet som vist i figuren nedenfor:

Underveisoppgave 1

To punkter er gitt ved \(A(-4, 1)\) og \(B(2, 5)\).

Bestem posisjonsvektorene til punktene \(A\) og \(B\).
Tegn posisjonsvektorene i et koordinatsystem.

Løsning

Posisjonsvektorene har de samme koordinatene som punktene i koordinatsystemet:

\[ \lvec{OA} = [-4, 1] \qog \lvec{OB} = [2, 5] \]

Vi kan tegne posisjonsvektorene som peker fra origo ut til punktene \(A\) og \(B\) i et koordinatsystem som vist nedenfor:

Vektorer mellom to punkter#

Vi skal se at vi kommer til å finne det spesielt nyttig å gå fra origo via et punkt \(A\) for å så gå videre til et punkt \(B\). Da trenger vi å vite hvordan vi bestemmer vektorer mellom to punkter i et koordinatsystem.

Når en vektor peker fra et punkt \(A\) til et punkt \(B\) i et koordinatsystem, kaller vi vektoren for \(\lvec{AB}\). Da tenker vi på vektoren som en pil som starter i \(A\) og slutter i \(B\).

Fra figuren til høyre kan vi forstå dette ved å tenke oss at vi enten går direkte til punktet \(B\) med \(\lvec{OB}\), eller så går vi først via \(A\) med \(\lvec{OA}\) og så videre til \(B\) med \(\lvec{AB}\). Begge veier må ende opp i samme punkt, så dermed er

\[ \lvec{OB} = \lvec{OA} + \lvec{AB} \liff \lvec{AB} = \lvec{OB} - \lvec{OA} \]

Vektorer mellom to punkter i et koordinatsystem

En vektor som peker fra et punkt \(A\) til et punkt \(B\) i et koordinatsystem, kaller vi for \(\lvec{AB}\).

Vektoren er da gitt ved

\[ \lvec{AB} = \lvec{OB} - \lvec{OA} \]

Vi tar altså vektoren som peker til punktet \(B\) og trekker fra vektoren som peker til punktet \(A\) for å finne vektoren som peker fra \(A\) til \(B\).

Eksempel 2

To punkter er gitt ved \(A(2, 3)\) og \(B(3, -1)\).

Bestem \(\lvec{AB}\).

Løsning

Vi har at

\[ \lvec{OA} = [2, 3] \qog \lvec{OB} = [3, -1] \]

Vektoren som peker fra \(A\) til \(B\) er da gitt ved

\[ \lvec{AB} = \lvec{OB} - \lvec{OA} = [3, -1] - [2, 3] = [3 - 2, -1 - 3] = [1, -4] \]

Underveisoppgave 2

To punkter er gitt ved \(A(-4, 1)\) og \(B(2, 5)\).

Bestem vektoren \(\lvec{AB}\) som peker fra \(A\) til \(B\).
Tegn vektoren \(\lvec{AB}\) i et koordinatsystem.

Løsning

Vi har at

\[ \lvec{OA} = [-4, 1] \qog \lvec{OB} = [2, 5] \]

Vektoren som peker fra \(A\) til \(B\) er da gitt ved

\[ \lvec{AB} = \lvec{OB} - \lvec{OA} = [2, 5] - [-4, 1] = [2 - (-4), 5 - 1] = [6, 4] \]

Vi kan tegne vektoren \(\lvec{AB}\) som peker fra punktet \(A\) til punktet \(B\) i et koordinatsystem som vist nedenfor:

Linjer i koordinatsystemet#

Når vi jobber med vektorer så ønsker vi i blant å beskrive linjer i et koordinatsystem ved hjelp av vektorer. Noen ganger bare for å gi en fullstendig beskrivelse av alle punkter som ligger på linja. I andre tilfeller vil vi bruke en beskrivelse av linjer for å flytte oss langs linja til vi finner et skjæringspunkt med et annet geometrisk objekt.

Når vi skal beskrive en linje \(\ell\) i et koordinatsystem, så trenger vi to ting:

Et startpunkt \(A\) som ligger på linja.
En retningsvektor \(\vec{v}\) som peker langs linja.

Vi trenger startpunktet så vi har et utgangspunkt for å bygge opp linja. Med retningsvektoren vet vi i hvilken retning vi må bevege oss fra startpunktet for å følge linja.

Parameterframstilling med vektorfunksjon#

-8.00 6.00

                t = 2.00
            

Når vi beskriver posisjonen til punktet på en linje \(\ell\) i et koordinatsystem kan vi bruke en vektorfunksjon \(\vec{r}(t)\). I første omgang vil \(t\) bare være en parameter (variabel), men når vi senere skal se på naturvitenskapelige anvendelser av vektorer, så vil \(t\) ofte representere tid.

For å bestemme posisjonen til et punkt \(P\) på linja, går vi veien om et punkt \(A\) med vektoren \(\lvec{OA}\) og så følger vi en retningsvektor \(\vec{v}\) som peker langs linja. Dersom vi følger retningsvektoren med \(t\) enheter ender vi opp i et punkt \(P(t)\) på linja som har posisjonsvektoren \(\vec{r}(t) = \lvec{OP}(t)\).

Den interaktive figuren til høyre lar deg undersøke hvordan posisjonsvektoren \(\vec{r}(t)\) endrer seg når vi varierer parameteren \(t\). Bruk den til å forstå beskrivelsen av linja \(\ell\) ved hjelp av posisjonsvektoren \(\vec{r}(t)\).

Linjer i koordinatsystemet (vektorfunksjon)

En linje \(\ell\) i et koordinatsystem kan beskrives ved hjelp av et startpunkt \(A\) som ligger på linja og en retningsvektor \(\vec{v}\) som peker langs linja. Da er alle punkter på linja gitt ved posisjonsvektoren \(\vec{r}(t)\) beskrevet av vektorfunksjonen

\[ \vec{r}(t) = \overrightarrow{OA} + \vec{v} \cdot t \]

Et annet punkt \(P(t)\) på linja finner vi ved å starte i \(A\) og bevege oss \(t\) enheter med retningsvektoren \(\vec{v}\). Dette tilsvarer å flytte oss fra \(A\) med \(\vec{v} \cdot t\).

For positive verdier av \(t\) går vi i samme retning som \(\vec{v}\), mens for negative verdier av \(t\) går vi i motsatt retning av \(\vec{v}\). Slik kan vi bygge opp linja i begge retninger, ved å starte i punktet \(A\) og bevege oss langs linja i retning av retningsvektoren \(\vec{v}\).

Vi tar et eksempel der vi må bestemme retningsvektoren ut ifra to punkter på linja.

Eksempel 3

En linje \(\ell\) går gjennom punktene \(A(2, 2)\) og \(B(4, 3)\).

Bestem posisjonsvektoren \(\vec{r}(t)\) for punktene på linja.

Løsning

Vi lar \(A(2, 2)\) være punktet på linja vi tar utgangspunkt i. Posisjonsvektoren til punktet \(A\) er da

\[ \lvec{OA} = [2, 2] \]

En retningsvektor \(\vec{v}\) for linja kan være vektoren som peker fra \(A\) til \(B\) siden begge disse punktene ligger på linja så \(\lvec{AB}\) vil peke langs linja. Da får vi at

\[ \vec{v} = \lvec{AB} = \lvec{OB} - \lvec{OA} = [4, 3] - [2, 2] = [2, 1] \]

Altså vil posisjonsvektoren \(\vec{r}(t)\) for punktene på linja være gitt ved

\[\begin{split} \begin{align*} \vec{r}(t) &= \overrightarrow{OA} + \vec{v} \cdot t \\ \\ &= [2, 2] + [2, 1] \cdot t \\ \\ &= [2, 2] + [2t, t] \\ \\ &= [2 + 2t, 2 + t] \qfor t \in \mathbb{R} \end{align*} \end{split}\]

Underveisoppgave 3

En linje \(\ell\) går gjennom punktene \(A(-1, 0)\) og \(B(2, 3)\).

Bestem posisjonsvektoren \(\vec{r}(t)\) for punktene på linja.

Fasit

\[ \vec{r}(t) = [-1 + 3t, 3t] \qfor t \in \mathbb{R} \]

Løsning

Vi lar \(A(-1, 0)\) være punktet på linja vi tar utgangspunkt i. Posisjonsvektoren til punktet \(A\) er da

\[ \lvec{OA} = [-1, 0] \]

En retningsvektor \(\vec{v}\) for linja kan være vektoren som peker fra \(A\) til \(B\) siden begge disse punktene ligger på linja så \(\lvec{AB}\) vil peke langs linja. Da får vi at

\[ \vec{v} = \lvec{AB} = \lvec{OB} - \lvec{OA} = [2, 3] - [-1, 0] = [3, 3] \]

Altså vil posisjonsvektoren \(\vec{r}(t)\) for punktene på linja være gitt ved

\[\begin{split} \begin{align*} \vec{r}(t) &= \overrightarrow{OA} + \vec{v} \cdot t \\ \\ &= [-1, 0] + [3, 3] \cdot t \\ \\ &= [-1, 0] + [3t, 3t] \\ \\ &= [-1 + 3t, 0 + 3t] \\ \\ &= [-1 + 3t, 3t] \qfor t \in \mathbb{R} \end{align*} \end{split}\]

Dersom vi kjenner til stigningstallet til en linje, så er det ganske enkelt å bestemme en retningsvektor for linja.

Retningsvektor og stigningstall

Hvis en linje \(\ell\) gitt ved \(y = ax + b\) har stigningstall \(a\), så vil en retningsvektor for linja være

\[ \vec{v} = [1, a] \]

Eksempel 4

En linje \(\ell\) er gitt ved likningen \(y = 2x - 4\).

Bestem posisjonsvektoren \(\vec{r}(t)\) for linja.

Løsning

Først kan vi se at stigningstallet til linja er \(a = 2\), som betyr at én retningsvektor for linja er gitt ved

\[ \vec{v} = [1, 2]. \]

Så trenger vi ett punkt på linja, som vi kan få ved å sette inn en verdi for \(x\) i likningen for linja. Vi velger \(x = 0\) som gir

\[ y = 2 \cdot 0 - 4 = -4. \]

Dermed er punktet \(A(0, -4)\) på linja. Da får vi at

\[\begin{split} \begin{align*} \vec{r}(t) &= \lvec{OA} + \vec{v} \cdot t \\ \\ &= [0, -4] + [1, 2] \cdot t \\ \\ &= [0, -4] + [t, 2t] \\ \\ &= [t, -4 + 2t] \end{align*} \end{split}\]

som gjelder for alle \(t \in \real\).

Underveisoppgave 4

En linje \(\ell\) er gitt ved likningen \(y = -\dfrac{1}{2}x + 3\).

Bestem posisjonsvektoren \(\vec{r}(t)\) for linja.

Fasit

\[ \vec{r}(t) = \left[t, 3 - \dfrac{1}{2}t\right] \qfor t \in \mathbb{R} \]

Løsning

Stigningstallet til linja er \(a = -\dfrac{1}{2}\) som betyr at en retningsvektor for linja er gitt ved

\[ \vec{v} = \left[1, -\dfrac{1}{2}\right]. \]

Vi trenger ett punkt på linja som vi finner ved å sette inn en \(x\)-verdi i likningen for linja. Vi velger \(x = 0\) som gir

\[ y = -\dfrac{1}{2} \cdot 0 + 3 = 3. \]

Dermed er punktet \(A(0, 3)\) på linja. Da får vi at

\[\begin{split} \begin{align*} \vec{r}(t) &= \lvec{OA} + \vec{v} \cdot t \\ \\ &= [0, 3] + \left[1, -\dfrac{1}{2}\right] \cdot t \\ \\ &= [0, 3] + \left[t, -\dfrac{1}{2}t\right] \\ \\ &= \left[t, 3 - \dfrac{1}{2}t\right] \end{align*} \end{split}\]

som gjelder for alle \(t \in \real\).

Parameterframstilling på komponentform#

En annen vanlig måte å beskrive linjer på er å skrive dem på komponentform. Dette er det samme som en vektorfunksjon, men representasjonen er skrevet som likninger for \(x\)- og \(y\)-koordinatene hver for seg, fremfor en samlet vektor.

Linjer i koordinatsystemet (parameterframstilling på komponentform)

En linje \(\ell\) i et koordinatsystem med vektorfunksjonen

\[ \vec{r}(t) = [x(t), y(t)] \]

kan skrives på komponentform gitt ved likningene

\[\begin{split} \ell: \begin{cases} x = x(t) \\ \\ y = y(t) \end{cases} \qfor t \in \mathbb{R} \end{split}\]

Eksempel 5

En linje \(\ell\) har vektorfunksjonen

\[ \vec{r}(t) = [2 + 2t, 2 + t] \qfor t \in \mathbb{R} \]

Bestem parameterframstillingen for linja.

Løsning

Vi kan se at

\[ x(t) = 2 + 2t \qog y(t) = 2 + t \]

Dermed er parameterframstillingen for linja \(\ell\) gitt ved

\[\begin{split} \ell: \begin{cases} x = 2 + 2t \\ \\ y = 2 + t \end{cases} \qfor t \in \mathbb{R} \end{split}\]

Underveisoppgave 5

En linje \(\ell\) har vektorfunksjonen

\[ \vec{r}(t) = [-1 + 3t, 3t] \qfor t \in \mathbb{R} \]

Bestem parameterframstillingen for linja.

Fasit

\[\begin{split} \ell: \begin{cases} x = -1 + 3t \\ \\ y = 3t \end{cases} \qfor t \in \mathbb{R} \end{split}\]

Løsning

Vi kan se at

\[ x(t) = -1 + 3t \qog y(t) = 3t \]

Dermed er parameterframstillingen for linja \(\ell\) gitt ved

\[\begin{split} \ell: \begin{cases} x = -1 + 3t \\ \\ y = 3t \end{cases} \qfor t \in \mathbb{R} \end{split}\]

Skjæring mellom to linjer#

Å finne skjæringspunktet mellom to linjer \(\ell\) med posisjonsvektor \(\vec{r}_\ell(t)\) og \(m\) med posisjonsvektor \(\vec{r}_m(s)\) i et koordinatsystem, kan vi finne ved å løse vektorlikningen

\[ \vec{r}_\ell(t) = \vec{r}_m(s) \]

Vektorlikningen vil gi oss et likningssystem fordi to vektorer er like når både \(x\)-komponenten og \(y\)-komponenten er like samtidig.

Når vi beskriver flere linjer i et koordinatsystem med vektorfunksjoner eller parameterframstillinger, så bruker vi forskjellige parametere \(t\) og \(s\) for de ulike linjene siden de teller bare antall “skritt” vi har tatt med hver retningsvektor. Siden retningsvektorene ikke trenger å være like lange, så vil ikke samme verdi av \(t\) og \(s\) gi like stor forflytning langs hver linje.

Skjæring mellom to linjer

La en linje \(\ell\) ha posisjonsvektoren \(\vec{r}_\ell(t)\) og en linje \(m\) ha posisjonsvektoren \(\vec{r}_m(s)\).

Skjæringspunktet mellom linjene finnes ved å løse vektorlikningen

\[ \vec{r}_\ell(t) = \vec{r}_m(s) \]

Eksempel 6

En linje \(\ell\) går gjennom punktene \(A(-4, -1)\) og \(B(2, 2)\).

En annen linje går gjennom punktet \(C(2, -1)\) og har retningsvektoren \(\vec{v}_m = [1, 2]\).

Bestem koordinatene til skjæringspunktet \(P\) mellom linjene.

Løsning

Vi starter med å lage posisjonsvektoren for linja \(\ell\). Vi har at retningsvektoren for linja er

\[ \vec{v}_\ell = \lvec{AB} = \lvec{OB} - \lvec{OA} = [2, 2] - [-4, -1] = [6, 3] \]

Vi velger å starte i punktet \(A(-4, -1)\), så posisjonsvektoren for linja \(\ell\) er da

\[ \vec{r}_\ell(t) = \lvec{OA} + \vec{v}_\ell \cdot t = [-4, -1] + [6, 3] \cdot t = [-4 + 6t, -1 + 3t] \qfor t \in \mathbb{R} \]

Retningsvektoren for linja \(m\) er gitt ved \(\vec{v}_m = [1, 2]\). Vi starter i punktet \(C(2, -1)\), så posisjonsvektoren for linja \(m\) er da

\[ \vec{r}_m(s) = \lvec{OC} + \vec{v}_m \cdot s = [2, -1] + [1, 2] \cdot s = [2 + s, -1 + 2s] \qfor s \in \mathbb{R} \]

Merk at vi her har brukt en annen parameter \(s\) for linja \(m\). Det er fordi vi allerede har brukt \(t\) for linja \(\ell\).

For å finne skjæringspunktet mellom linjene løser vi vektorlikningen

\[ \vec{r}_\ell(t) = \vec{r}_m(s) \]

som gir vektorlikningen

\[ [-4 + 6t, -1 + 3t] = [2 + s, -1 + 2s] \]

Siden \(x\)-komponenten og \(y\)-kompontene må være like samtidig, får vi likningssystemet

\[ -4 + 6t = 2 + s \and -1 + 3t = -1 + 2s \]

Vi løser likningssystemet med CAS:

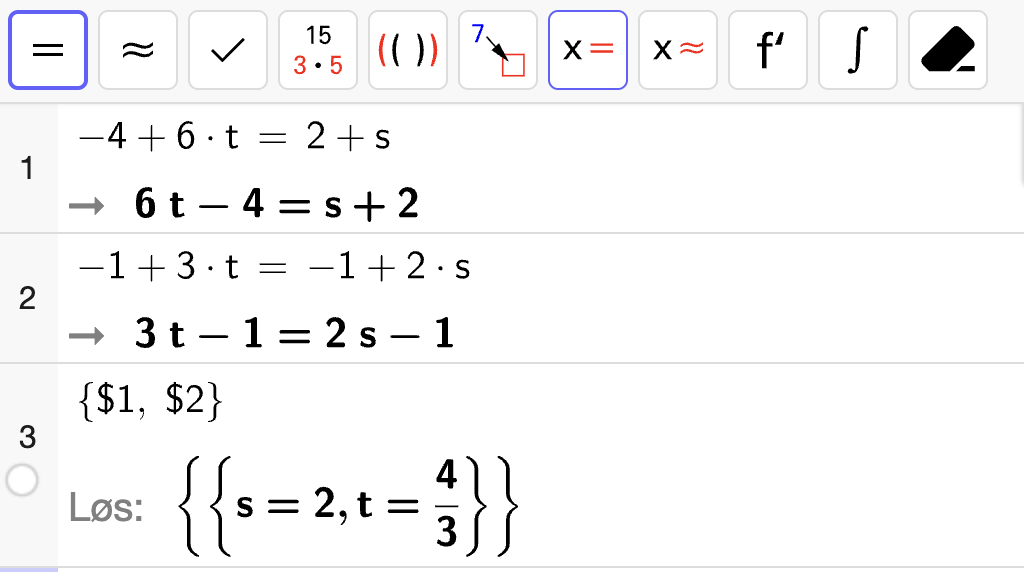
Altså er

\[ s = 2 \and t = \dfrac{4}{3} \]

For å finne koordinatene til skjæringspunktet \(P\), kan vi bruke enten \(\vec{r}_\ell(t)\) eller \(\vec{r}_m(s)\). Vi bruker \(\vec{r}_m(s)\):

\[ \vec{r}_m(2) = [2 + 2, -1 + 2 \cdot 2] = [4, 3] \]

Altså er koordinatene til skjæringspunktet \(P\) gitt ved \(P(4, 3)\).

Vi kan dobbeltsjekke at vi får det samme svaret med \(\vec{r}_\ell(t)\):

\[ \vec{r}_\ell\left(\dfrac{4}{3}\right) = \left[-4 + 6 \cdot \dfrac{4}{3}, -1 + 3 \cdot \dfrac{4}{3}\right] = [4, 3] \]

Svarene stemmer overens.

Underveisoppgave 6

En linje \(\ell\) går gjennom punktet \(A(-1, 0)\) og har retningsvektoren \(\vec{v}_\ell = [3, 3]\).

En annen linje \(m\) går gjennom punktene \(B(2, 3)\) og \(C(5, 0)\).

Bestem koordinatene til skjæringspunktet mellom linjene.

Fasit

\[ (2, 3) \]

Løsning

Vi bestemmer posisjonsvektoren til \(\ell\) ved å starte i punktet \(A(-1, 0)\):

\[ \vec{r}_\ell(t) = \lvec{OA} + \vec{v}_\ell \cdot t = [-1, 0] + [3, 3] \cdot t = [-1 + 3t, 3t] \qfor t \in \mathbb{R} \]

Så bestemmer vi retningsvektoren for linja \(m\) ved å bruke punktene \(B(2, 3)\) og \(C(5, 0)\):

\[ \vec{v}_m = \lvec{BC} = \lvec{OC} - \lvec{OB} = [5, 0] - [2, 3] = [3, -3] \]

Vi lager posisjonsvektoren for linja \(m\) ved å starte i punktet \(B(2, 3)\):

\[ \vec{r}_m(s) = \lvec{OB} + \vec{v}_m \cdot s = [2, 3] + [3, -3] \cdot s = [2 + 3s, 3 - 3s] \qfor s \in \mathbb{R} \]

For å finne skjæringspunktet mellom linjene løser vi vektorlikningen

\[ \vec{r}_\ell(t) = \vec{r}_m(s) \]

som gir vektorlikningen

\[ [-1 + 3t, 3t] = [2 + 3s, 3 - 3s] \]

Siden \(x\)-komponenten og \(y\)-kompontene må være like samtidig, får vi likningssystemet

\[ -1 + 3t = 2 + 3s \and 3t = 3 - 3s \]

Vi tar \(3t = 3 - 3s\) fra den andre likningen og setter inn i den for \(3t\) i den første likningen:

\[ -1 + (3 - 3s) = 2 + 3s \]

Så forenkler vi og løser for \(s\):

\[\begin{split} 2 - 3s = 2 + 3s \\ \\ -3s - 3s = 2 - 2 \\ \\ -6s = 0 \\ \\ s = 0 \end{split}\]

Det holder å bestemme \(s\) for å bestemme skjæringspunktet. Vi setter \(s = 0\) inn i posisjonsvektoren til linja \(m\) for å finne koordinatene til skjæringspunktet:

\[ \vec{r}_m(0) = [2 + 3 \cdot 0, 3 - 3 \cdot 0] = [2, 3] \]

Altså er koordinatene til skjæringspunktet mellom linjene gitt ved \((2, 3)\).

Vektorer i koordinatsystemet med digitale verktøy#

Når vi jobber med vektorer i CAS, så skiller ikke CAS på punkter og vektorer. Nedenfor er en oversikt over kommandoer og skrivemåter for å regne ut ulike størrelser med vektorer i CAS:

Vektorer#

I Utforsk 1 nedenfor vil du lære de mest brukte kommandoene og skrivemåtene vi trenger for å jobbe med vektorer i CAS.

Utforsk 1

Bruk CAS-vinduet til å øve på å bruke kommandoene og skrivemåtene som vises i gif-ene i hver del.

a

I gif-en nedenfor definerer vi posisjonsvektoren til punktene \(A(2, 3)\) og \(B(3, -1)\) i CAS.

Legg merke til at når vi skriver med store bokstaver så får vi et punkt \((2, 3)\), men når vi skriver med små bokstaver får vi \(\mqty(2 \\ 3)\) som representerer en vektor. De vil se forskjellige ut i grafikkvinduet, men i praksis er dette pynt og gjør ingen forskjell for regningen som skjer i CAS.

b

I gif-en nedenfor regner vi ut lengden til en vektor \(\vec{a} = [-3, 4]\) i CAS på to måter.

Ved å skrive \(|\vec{a}|\).
Ved å bruke kommandoen Lengde(Liste).

Begge kommandoer gir samme svar. Prøv selv med CAS-vinduet!

c

Gitt to punkter \(A(-2, 3)\) og \(B(4, 1)\). I gif-en nedenfor bestemmer vi

Vektoren \(\lvec{AB}\) som peker fra \(A\) til \(B\).
Lengden til vektoren \(\lvec{AB}\).

Prøv selv med CAS-vinduet!

../../../_images/vektorer_mellom_to_punkter.webp

Vektorfunksjoner for linjer#

I Utforsk 2 nedenfor vil du lære hvordan vi jobber med vektorfunksjoner i CAS.

Utforsk 2

Bruk CAS-vinduet til å øve på å bruke kommandoene og skrivemåtene som vises i gif-ene i hver del.

a

En linje \(\ell\) går gjennom punktet \(A(1, 2)\) og har retningsvektoren \(\vec{v} = [3, 4]\).

I gif-en nedenfor bestemmer vi

posisjonsvektoren \(\vec{r}(t)\) for linja
regner ut punktet på linja når \(t = 2\).

Prøv selv med CAS-vinduet!

b

En linje \(\ell\) går gjennom punktene \(A(-2, 1)\) og \(B(4, 2)\).

I gif-en nedenfor bestemmer vi

En retningsvektor \(\vec{v} = \lvec{OB} - \lvec{OA}\) for linja ved å bruke punktene \(A\) og \(B\).
posisjonsvektoren \(\vec{r}(t)\) for linja.

Prøv selv med CAS-vinduet!

c

To linjer \(\ell\) og \(m\) har posisjonsvektorene gitt nedenfor

\[ \vec{r}_\ell(t) = [1 + 2t, 3t] \qog \vec{r}_m(s) = [4 + s, 2 - s] \]

I gif-en nedenfor bestemmer vi skjæringspunktet mellom linjene ved å løse vektorlikningen

\[ \vec{r}_\ell(t) = \vec{r}_m(s) \]

Prøv selv med CAS-vinduet!

../../../_images/skj%C3%A6ring_mellom_linjer.webp