Oppgaver: Optimering

8. Oppgaver: Optimering#

Å løse oppgavene nedenfor uten hjelpemidler kan være veldig tidkrevende. Det er derfor lurt å løse dem ved å bruke CAS.

Oppgave 1

Anna og Bjørn har materiale nok til å lage et gjerde som er 64 m langt.

De skal gjerde inn et område som skal ha form som et rektangel, og de ønsker at området skal få størst mulig areal. Se figuren nedenfor.

Bestem det største mulige arealet de kan gjerde inn.

Fasit

\[ A_\text{størst} = 256 \, \mathrm{m}^2 \]

Løsning

Omkretsen til området kan beskrives som:

\[ 2x + 2y = 64 \liff x + y = 32 \]

Arealet til området vil være $A = x \cdot y$. Vi kan løse likningen ovenfor for $y$:

\[ x + y = 32 \liff y = 32 - x \]

Da kan vi lage en funksjon $A(x)$ for arealet som blir:

\[ A(x) = x\cdot y(x) = x\cdot(32 - x) = -x^2 + 32x \]

For å bestemme den verdien av $x$ som gir størst areal, så må vi se etter ekstremalpunktene til $A$. Deretter må vi sjekke at $A''(x) < 0$ i punktet for å sikre at det er et toppunkt. Vi bruker CAS til å utføre selve regningen:

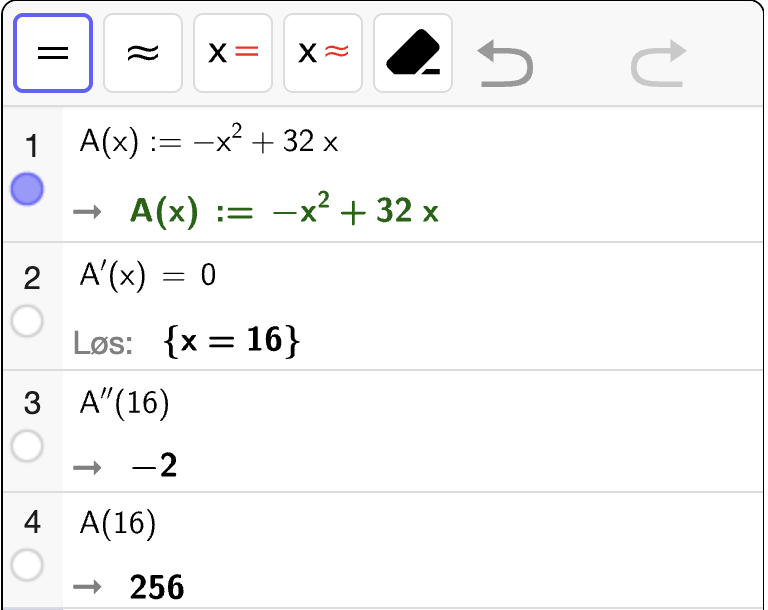
Vi ser at $A'(x) = 0$ når $x = 16$. Vi ser også at $A''(16) < 0$ som betyr at $A$ er konkav frown polynomial icon i nabolaget til punktet. Dermed gir $x = 16$ et toppunkt. Vi ser at da er $A(16) = 256$ som betyr at det største mulige arealet er $256 \, \mathrm{m}^2$.

Oppgave 2

Anna og Bjørn skal slå opp telt ved en elvebredde. De skal sette opp et tau rundt teltet for å holde dyr unna.

De har 80 m med tau og fire pinner. Området de skal gjerde inn skal ha form som et rektangel og de tenker å bruke elvebredden som en av sidene i rektangelet slik at de kan gjerde inn et større område. Målet deres er å få et størst mulig areal innenfor gjerdet. Se figuren nedenfor.

Bestem det største mulige arealet de kan gjerde inn.

Fasit

\[ A_\mathrm{størst} = 800 \, \mathrm{m}^2 \]

Løsning

Vi setter opp et uttrykk for “omkretsen” av gjerde:

\[ x + 2y = 80 \]

Dette kan vi løse for $y$:

\[ x + 2y = 80 \liff y = 40 - \dfrac{1}{2}x \]

Nå kan vi lage en funksjon $A(x)$ for arealet som blir:

\[ A(x) = x \cdot y(x) = x \cdot \left(40 - \dfrac{1}{2}x\right) = -\dfrac{1}{2}x^2 + 40x \]

For å bestemme ekstremalpunktene til $A$, så må vi løse $A'(x) = 0$ og sjekke at $A''(x) < 0$ i punktet for å sikre at det er et toppunkt. Vi bruker CAS til å utføre selve regningen:

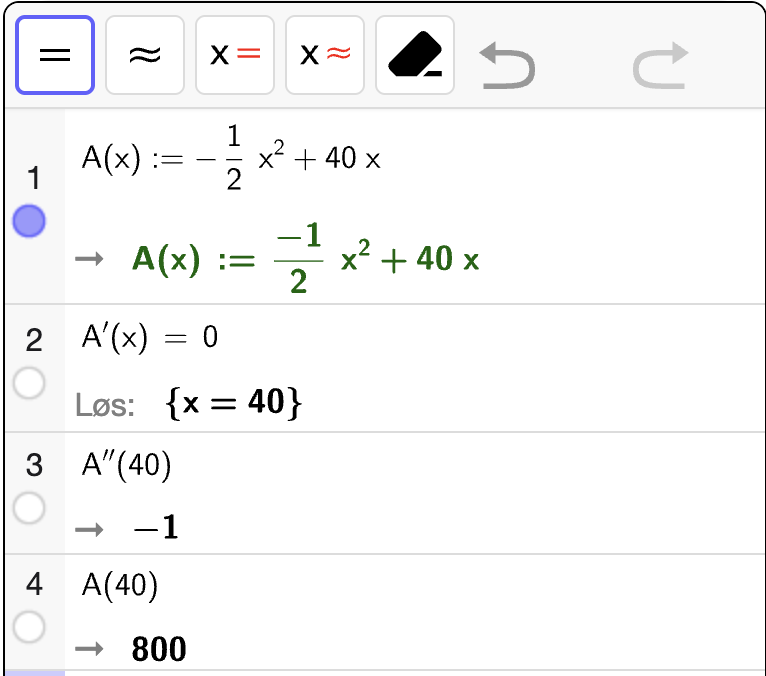
Fra utskriften ser vi at $x = 40$ er et ekstremalpunkt siden $A'(40) = 0$. Videre er punktet et toppunkt siden $A''(40) < 0$. Dermed gir $x = 40$ et toppunkt. Vi ser også at $A(40) = 800$ som betyr at det største mulige arealet er $800 \, \mathrm{m}^2$.

Oppgave 3

En andregradsfunksjon $f$ er gitt ved

\[ f(x) = -x^2 + 9 \qder x \in [0, 3]. \]

En trekant har hjørner i $(0, 0)$, $(k, 0)$ og $(k, f(k))$. Se figuren nedenfor.

Bestem $k$ slik at arealet av trekanten er størst mulig.

Fasit

\[ k = \sqrt{3} \]

Løsning

Vi setter opp et funksjon $A(k)$ for arealet av trekanten:

\[ A(k) = \dfrac{k \cdot f(k)}{2} = \dfrac{-k^3 + 9k}{2} = -\dfrac{1}{2}k^3 + \dfrac{9}{2}k \]

For å bestemme ekstremalpunktene til arealfunksjonen, så må vi løse $A'(k) = 0$ og sjekke at $A''(k) < 0$ i punktet for å sikre at det er et toppunkt. Vi bruker CAS til å utføre selve regningen:

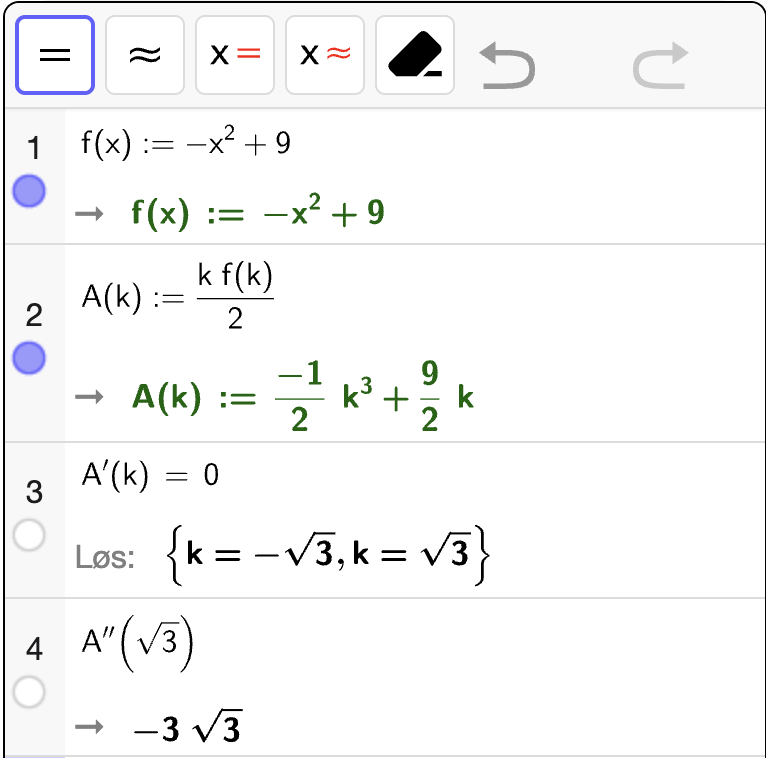
Vi får to løsninger til likningen $A'(k) = 0$, men det er bare $k = \sqrt{3}$ som er en del av definisjonsmengden. Vi ser også at $A''(\sqrt{3}) < 0$ som betyr at $A$ er konkav frown polynomial icon i nabolaget til punktet. Dermed gir $k = \sqrt{3}$ et toppunkt. Dermed blir arealet av trekanten størst mulig dersom

\[ k = \sqrt{3} \]

Oppgave 4

Nedenfor ser du grafen til en funksjon $f$ gitt ved

\[ f(x) = \dfrac{8}{x^2 + 20} \qder D_f = [0, \to \rangle \]

Et rektangel har hjørnene $(0, 0)$, $(r, 0)$, $(r, f(r))$ og $(0, f(r))$. Se figuren nedenfor.

Bestem $r$ slik at arealet av rektangelet er størst mulig.

Fasit

\[ r = 2\sqrt{5} \]

Løsning

Vi bestemmer en funksjon $A(r)$ for arealet av rektangelet:

\[ A(r) = r\cdot f(r) = r \cdot \dfrac{8}{r^2 + 20} = \dfrac{8r}{r^2 + 20} \]

For å bestemme ekstremalpunktene til $A$, må vi løse $A'(r) = 0$ og sjekke at $A''(r) < 0$ i punktet for å sikre at det er et toppunkt. Vi bruker CAS til å utføre selve regningen:

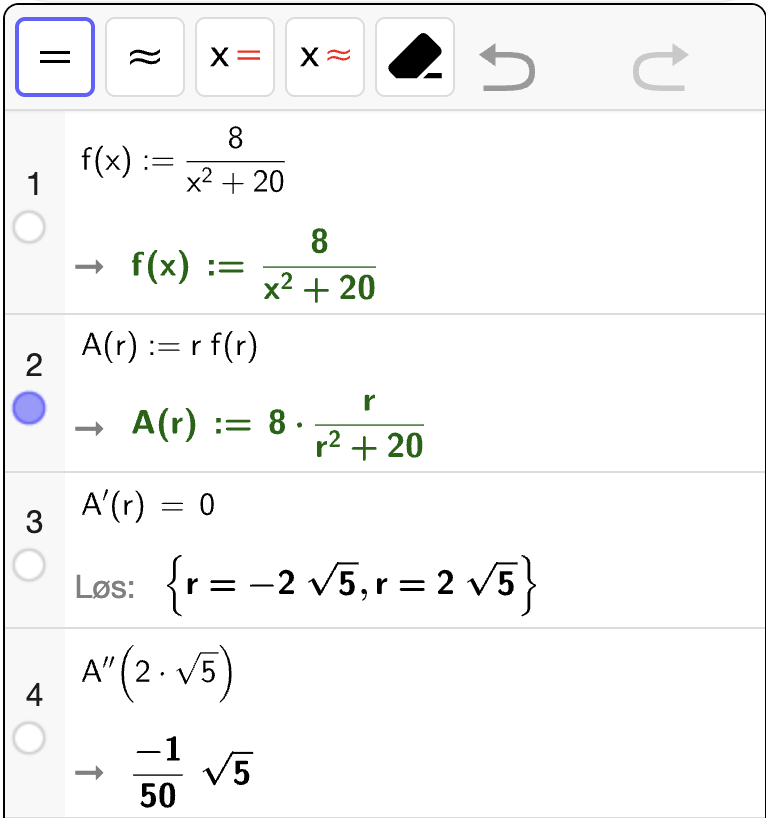
Fra utskriften er vi at $A'(r) = 0$ når $r = 2\sqrt{5}$ (som er den eneste løsningen som er innenfor definisjonsmengden). Vi ser også at $A''(2\sqrt{5}) < 0$ som betyr at $A$ er konkav frown polynomial icon i nabolaget til punktet. Dermed gir $r = 2\sqrt{5}$ et toppunkt. Derfor vil $r = 2\sqrt{5}$ gi det største arealet av rektangelet.

Oppgave 5

Punktene på en halvsirkel oppfyller likningen

\[ x^2 + y^2 = 4 \qder y \geq 0. \]

Et rektangel har hjørnene $(-x, 0)$, $(x, 0)$, $(x, f(x))$ og $(-x, f(-x))$ der $f$ er grafen til halvsirkelen.

Se figuren nedenfor.

Bestem $x$ slik at arealet av rektangelet er størst mulig.

Fasit

\[ x = \sqrt{2} \]

Løsning

Vi starter med å bestemme en funksjon $A(x)$ som gir arealet av rektangelet. Denne vil være gitt ved:

\[ A(x) = 2x \cdot f(x) \]

Vi trenger et uttrykk for $f(x)$ som vi kan bestemme ved å løse likningen for halvsirkelen for $y$:

\[ x^2 + y^2 = 4 \liff y^2 = 4 - x^2 \limplies y = \sqrt{4 - x^2} \]

Dermed vil $y(x) = \sqrt{4 - x^2}$. Vi kan dermed skrive arealfunksjonen som:

\[ A(x) = 2xy(x) = 2x \cdot \sqrt{4 - x^2} \]

For å bestemme ekstremalpunktene til $A$, må vi løse $A'(x) = 0$ og sjekke at $A''(x) < 0$ i punktet for å sikre at det er et toppunkt. Vi bruker CAS til å utføre selve regningen:

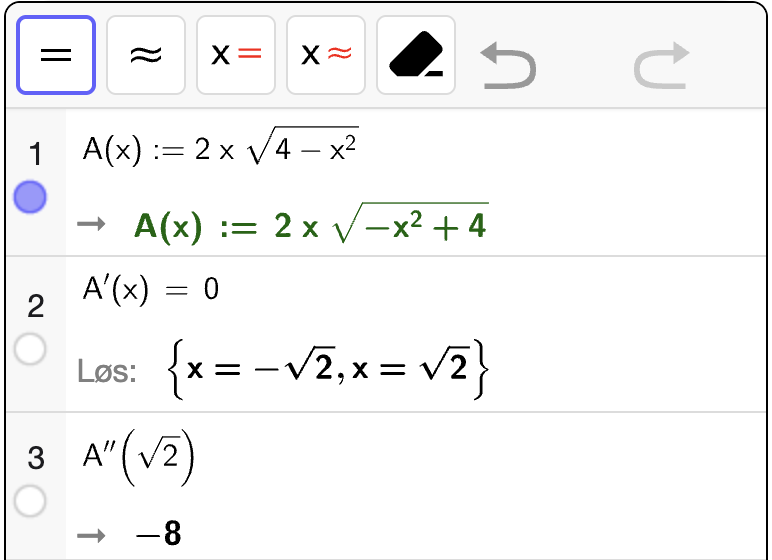
Vi ser at $A'(x) = 0$ når $x = \sqrt{2}$. Videre er $A''(\sqrt{2}) < 0$ som betyr at $A$ er konkav frown polynomial icon i nabolaget til punktet. Dermed gir $x = \sqrt{2}$ et toppunkt. Derfor vil $x = \sqrt{2}$ gi det største arealet av rektangelet.

Oppgave 6

Anna skal reise fra en holme som ligger $8$ km fra strandkanten. $12$ km fra det punktet på stranden som ligger nærmest holmen, ligger det en hytte. Anna kan ro med en fart på $2$ km/t og gå med en fart på $6$ km/t. Anna kan gå i land i hvilket som helst punkt $\ell$ på veien.

Se figuren nedenfor.

Fasit

\[ x = 2\sqrt{2} \, \mathrm{km} \]

Løsning

Tiden Anna bruker vil være gitt ved strekningen $s$ hun reiser delt på farten $v$ hun har. Strekningen hun må ro før hun går i land er

\[ s_\mathrm{vann}(x) = \sqrt{x^2 + 8^2} = \sqrt{x^2 + 64} \]

Strekningen Anna må gå når hun er i land er

\[ s_\mathrm{land}(x) = 12 - x \]

Tiden Anna vil bruke på hver del av turen blir dermed:

\[ T_\mathrm{vann}(x) = \dfrac{s_\mathrm{vann}}{v_\mathrm{vann}} = \dfrac{\sqrt{x^2 + 64}}{2} \and T_\mathrm{land}(x) = \dfrac{s_\mathrm{land}}{v_\mathrm{land}} = \dfrac{12 - x}{6} \]

Den samlede tiden kan derfor beskrives av funksjonen

\[ T(x) = T_\mathrm{vann}(x) + T_\mathrm{land}(x) = \dfrac{\sqrt{x^2 + 64}}{2} + \dfrac{12 - x}{6} \]

For å få kortest mulig tid, må vi bestemme ekstremalpunktene til $T$. Da løser vi $T'(x) = 0$ og sjekker at $T''(x) > 0$ i punktet:

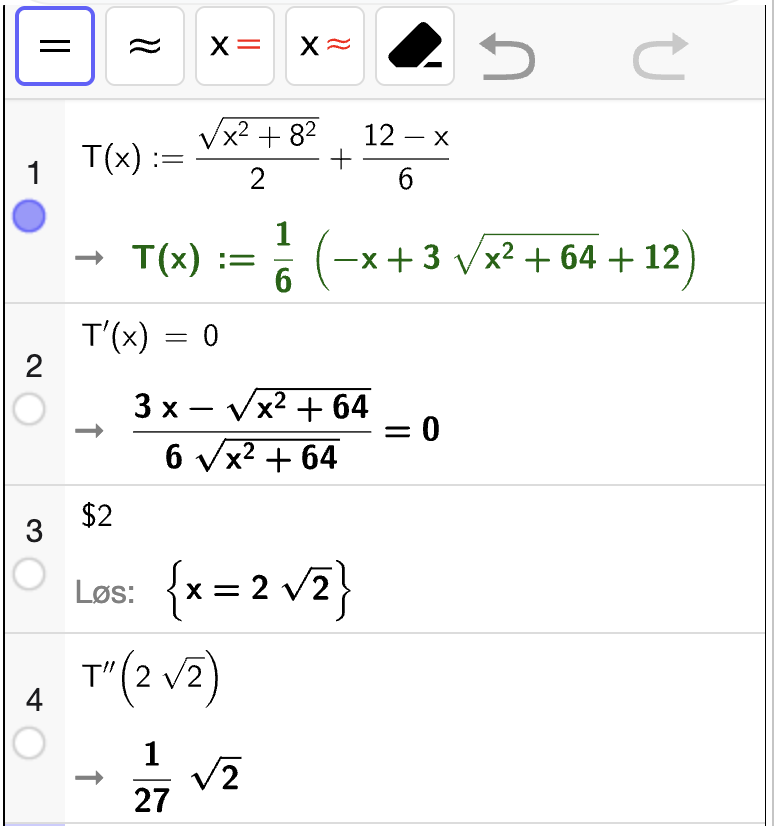
Vi ser at $T'(x) = 0$ når $x = 2\sqrt{2}$. Vi ser også at $T''(2\sqrt{2}) > 0$ som betyr at punktet gir et bunnpunkt. Derfor må Anna gå i land $2\sqrt{2}$ km fra det punktet på stranden som ligger nærmest holmen for å få kortest mulig reisetid.

Oppgave 7

En takrenne skal lages i form av et åpent trapes ved å brette to sidekanter fra et flatt rektangel slik at alle sidelengder i takrenna er $10$ cm og takrennen har en høyde på $x$ cm. Se figuren nedenfor.

Bestem høyden $x$ slik at mest mulig vann kan strømme gjennom takrenna.

Fasit

\[ 5 \sqrt{3} \, \mathrm{cm} \]

Løsning

For at mest mulig vann skal strømme gjennom, må arealet av tverrsnittet til takrenna være størst mulig. Vi bestememr en funksjon for arealet:

\[ A(x) = 10x + x\sqrt{10^2 - x^2} = 10x + x\sqrt{100 - x^2} \]

Vi må finne ekstremalpunktene til $A$. Da må vi løse $A'(x) = 0$ og sjekke om løsningen gir et toppunkt. Vi bruker CAS til å utføre selve regningen:

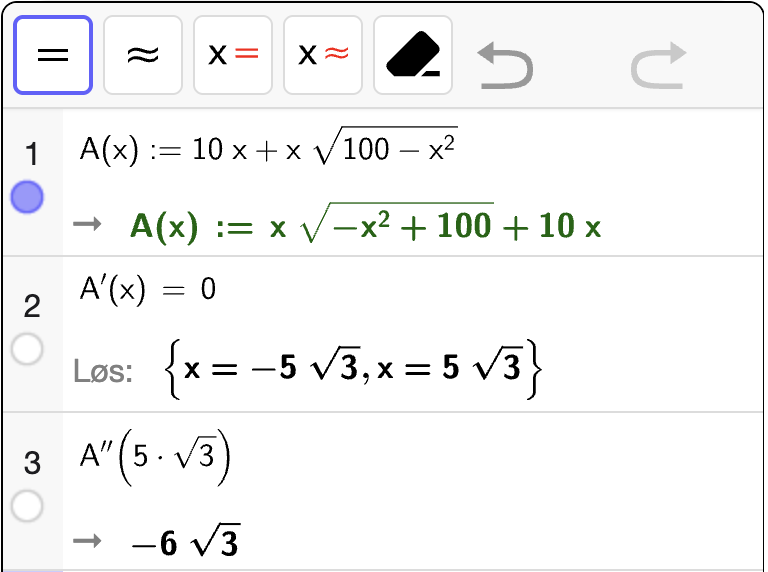
Fra utskriften ser vi at $A'(x) = 0$ når

\[ x = \pm 5 \sqrt{3} \]

Det er bare den positive løsningen som gir mening. I tillegg så er $A''(5\sqrt{3}) < 0$ som betyr at $A$ er konkav frown polynomial icon i nabolaget til punktet. Dermed gir $x = 5\sqrt{3}$ et toppunkt for $A$. Derfor vil det strømme mest vann gjennom takrenna dersom høyden er $5 \sqrt{3} \, \mathrm{cm}$.

Oppgave 8

En sylinder har overflateareal $A = 32\pi$.

Bestem hvilken høyde $h$ og radius $r$ som gir sylinderen størst mulig volum.

Fasit

\[ r = \dfrac{4\sqrt{3}}{3} \and h = \dfrac{8\sqrt{3}}{3} \]

Løsning

Overflatearealet $A$ kan uttrykkes som

\[ A = 2\pi r^2 + 2\pi rh = 32\pi \]

Volumet er gitt ved

\[ V = \pi r^2 h \]

Vi kan bestemme en funksjon $V(r)$ eller en funksjon $V(h)$ ved å bruke likningen for overflatearealet. Siden $r^2$ opptrer i begge uttrykk, er det enklere å løse likningen for overflatearealet for $h$ og erstatte dette i uttrykket for volumet $V$:

\[ 2\pi r^2 + 2\pi r h = 32\pi \]

\[ r^2 + rh = 16 \]

\[ rh = 16 - r^2 \liff h(r) = \dfrac{16 - r^2}{r} \]

Så setter vi uttrykket for $h$ inn i uttrykket for volumet:

\[ V(r) = \pi r^2 h(r) = \pi r^2 \cdot \dfrac{16 - r^2}{r} = \pi r(16 - r^2) = \pi(16r - r^3) \]

For å bestemme ekstremalpunktene til $V$, må vi løse $V'(r) = 0$ og sjekke at $V''(r) < 0$ i punktet for å sikre at det er et toppunkt. Vi bruker CAS til å utføre selve regningen:

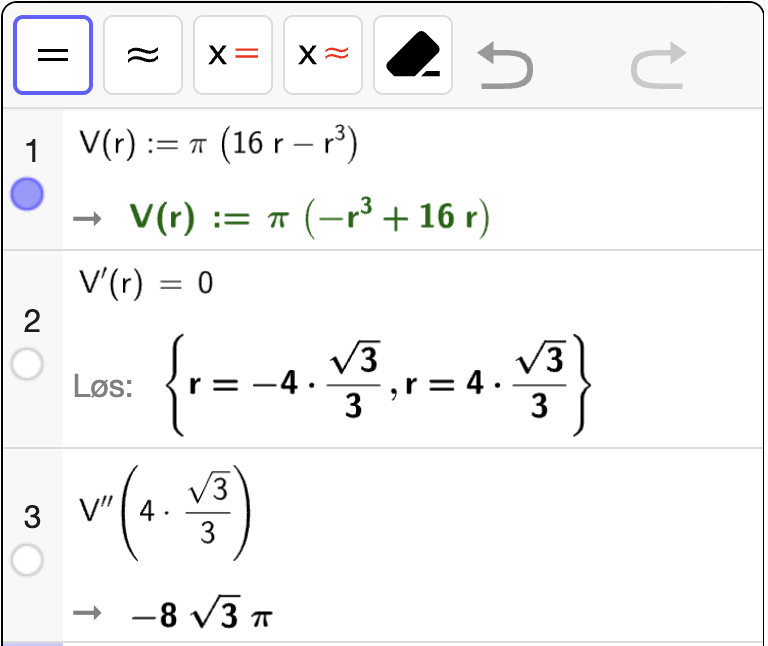
Vi ser at $V'(r) = 0$ når $x = \dfrac{4\sqrt{3}}{3}$. Vi ser også at $V''\left(\dfrac{4\sqrt{3}}{3}\right) < 0$ som betyr at $V$ er konkav frown polynomial icon i nabolaget til punktet. Dermed gir $r = \dfrac{4\sqrt{3}}{3}$ et toppunkt. Vi trenger også høyden ved denne radien, så vi også kan regne ut med CAS:

Dermed er volumet størst mulig hvis

\[ r = \dfrac{4\sqrt{3}}{3} \and h = \dfrac{8\sqrt{3}}{3} \]

Oppgave 9

En kurve er gitt ved grafen til funksjonen $f(x) = x^2$. I samme figur er et punkt $P(6, 3)$. Et linjestykke $\ell$ går fra punktet $P$ til et punkt på grafen.

Bestem koordinatene til punktet på grafen som gjør at $\ell$ blir kortest mulig. Bestem et eksakt uttrykk for lengden av $\ell$ i dette tilfellet.

Fasit

Koordinatene til punktet på grafen er $(2, 4)$
Lengden til linjestykket er da $\sqrt{17}$

Løsning

Avstanden fra punktet $P(6, 3)$ til et punkt på grafen $(x, f(x))$ kan vi uttrykke ved hjelp av Pytagoras’ setning:

\[ d(x) = \sqrt{(x - 6)^2 + (f(x) - 3)^2} = \sqrt{(x - 6)^2 + (x^2 - 3)^2} \]

For å bestemme ekstremalpunktene til $d$, må vi løse $d'(x) = 0$ og sjekke at $d’'(x) > 0 i punktet for å sikre at det er et bunnpunkt. Vi bruker CAS til å utføre selve regningen:

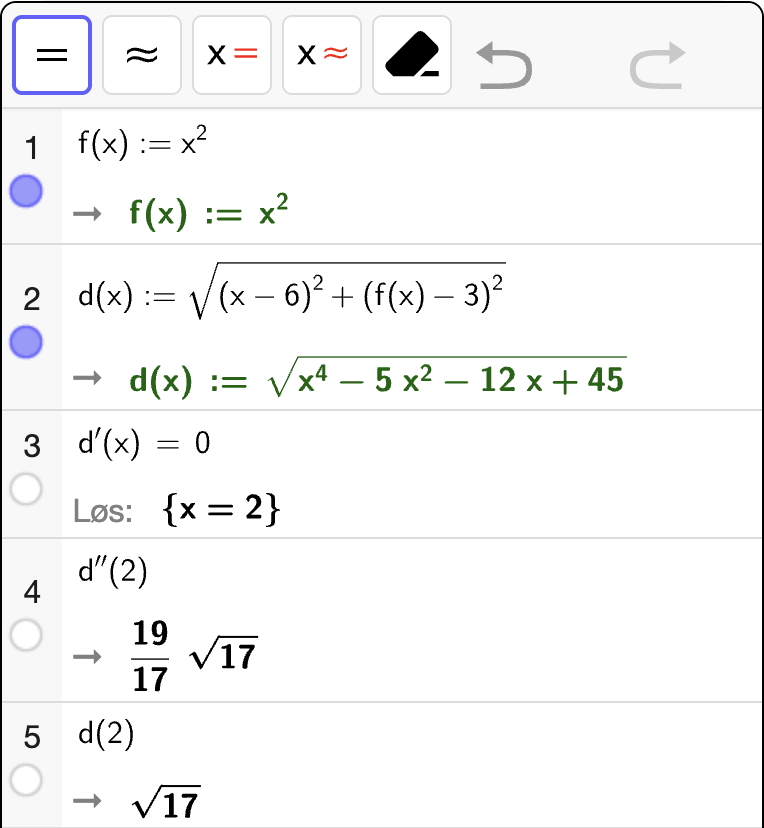
Vi ser at $d'(x) = 0$ når $x = 2$. Vi ser også at $d''(2) > 0$ som betyr at $d$ er konveks smile polynomial icon i nabolaget til punktet. Dermed gir $x = 2$ et bunnpunkt. Derfor vil linjestykket $\ell$ bli kortest mulig når det går fra $P(6, 3)$ til punktet $(2, f(2)) = (2, 4)$ på grafen. Vi ser også at $d(2) = \sqrt{17}$ som er lengden av linjestykket i dette tilfellet.

Oppgave 10

Punktene på en parabel tilfredsstiller likningen

\[ x = (y - 1)^2 - 2. \]

Kurven til parabelen er vist i figuren nedenfor.

Bestem en eksakt verdi for den korteste avstanden fra punktet $P(-2, 4)$ til kurven.

Fasit

\[ \sqrt{5} \]

Løsning

Avstanden fra punktet $P(-2, 4)$ til et punkt på parabelen $(x, y)$ kan vi uttrykke ved hjelp av Pytagoras’ setning:

\[\begin{align*} d &= \sqrt{(x + 2)^2 + (y - 4)^2} = \sqrt{\left((y - 1)^2 - 2 + 2\right)^2 + (y - 4)^2} \\ \\ &= \sqrt{(y - 1)^4 + (y - 4)^2} \end{align*}\]

Vi har derfor en funksjon $d(y)$ for avstanden fra punktet $P$ til et punkt på parabelen. Vi må finne ekstremalpunktene til $d$. Da må vi løse $d'(y) = 0$ og sjekke at løsningen gir et bunnpunkt for at vi skal få kortest mulig avstand. Vi gjør dette med CAS:

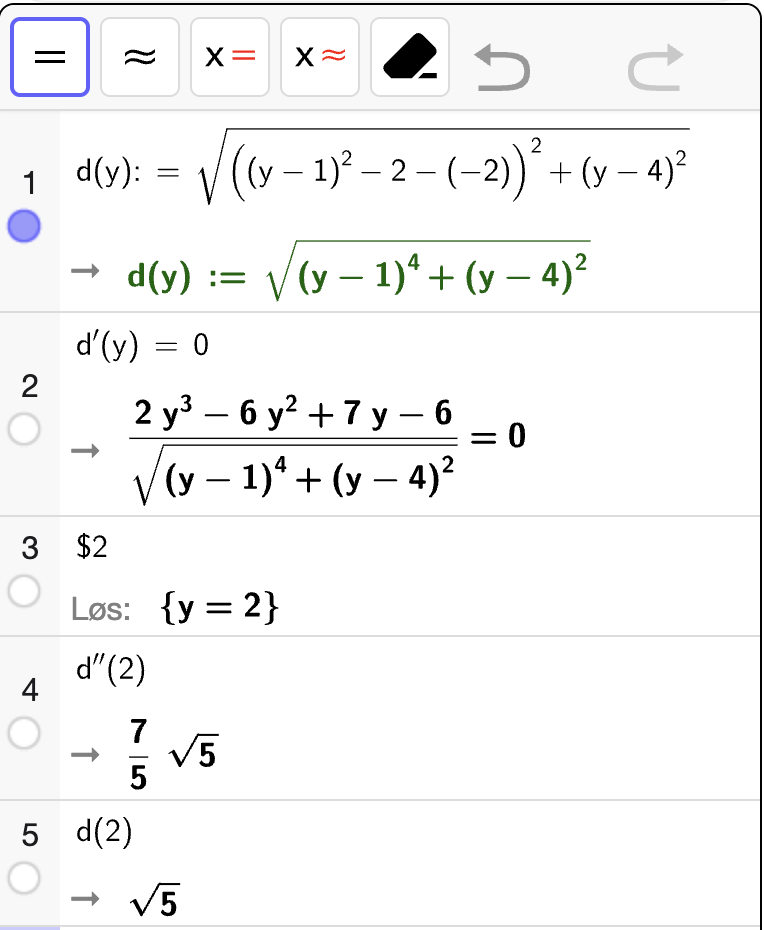
Fra utskriften ser vi at $d'(y) = 0$ når $y = 2$. Da er $d''(2) > 0$ som betyr at $d$ er konveks smile polynomial icon i nabolaget til punktet. Dermed gir $y = 2$ et bunnpunkt. Derfor vil den korteste avstanden fra punktet $P(-2, 4)$ til kurven være når vi går til punktet på kurven der $y = 2$. Fra utskriften ser vi at $d(2) = \sqrt{5}$ som er den korteste avstanden.

Oppgave 11

Et punkt $A$ ligger en avstand $2$ fra en linje $\ell$. Et annet punkt $C$ ligger en avstand $4$ fra linjen $\ell$.

Et punkt $B$ skal plasseres på $\ell$ slik at summen av linjestykkene $AB + BC$ blir minst mulig.

Se figuren nedenfor.

Bestem den minste verdien for summen av linjestykkene $AB + BC$.

Fasit

\[ 3\sqrt{13} \]

Løsning

Vi lar $x$ være avstanden fra det punktet på linja $\ell$ som ligger nærmest $A$ bort til punktet $B$. Da vil avstanden fra $B$ bort til det punktet på $\ell$ som ligger nærmest $C$ være $9 - x$. Bruker vi Pytagoras’ setning, får vi da at linjestykket $AB$ er:

\[ AB = \sqrt{x^2 + 2^2} = \sqrt{x^2 + 4} \]

På tilsvarende vis vil linjestykket $BC$ være

\[ BC = \sqrt{(9 - x)^2 + 4^2} = \sqrt{(x - 9)^2 + 16} \]

Vi kan lage en funksjon $L(x)$ som gir summen av de to linjestykkene:

\[ L(x) = AB + BC = \sqrt{x^2 + 4} + \sqrt{(x - 9)^2 + 16} \]

For å bestemme ekstremalpunktene til $L$, må vi løse $L'(x) = 0$ og sjekke at $L’'(x) > 0 i punktet for å sikre at det er et bunnpunkt. Vi bruker CAS til å utføre selve regningen:

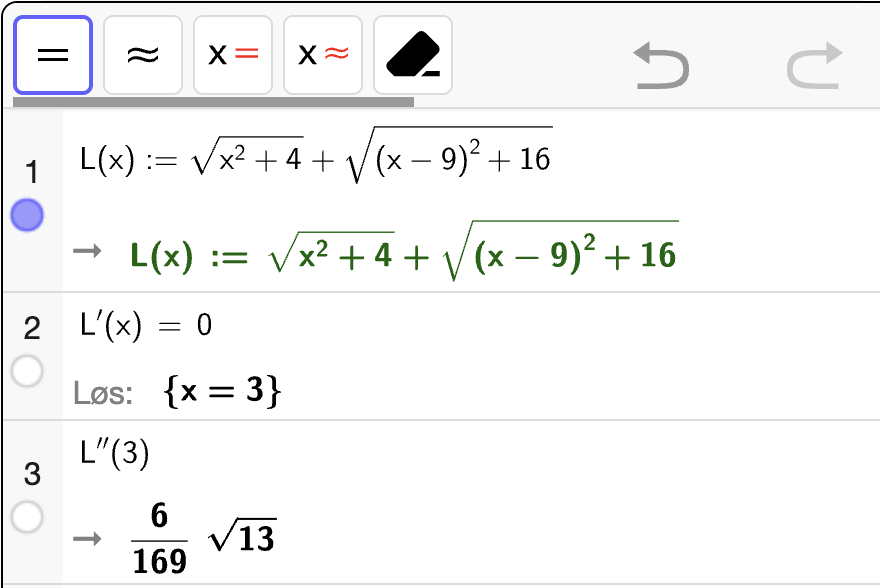
Vi ser at $L'(x) = 0$ når $x = 3$. Vi ser også at $L''(3) > 0$ som betyr at $L$ er konveks smile polynomial icon i nabolaget til punktet. Dermed gir $x = 3$ et bunnpunkt. Derfor vil summen av linjestykkene $AB + BC$ bli minst mulig når $B$ ligger $3$ enheter fra punktet på linja $\ell$ som ligger nærmest $A$. Vi kan også regne ut den minste verdien for summen av linjestykkene i dette tilfellet (med CAS):

Altså er den minste verdien for summen av linjestykkene $AB + BC$ lik $3\sqrt{13}$.

Oppgave 12

En likebeint trekant skal innskrives i en sirkel med radius $1$.

Bestem en eksakt verdi for det største arealet en slik trekant kan ha.

Vanskelig å komme i gang? Her er en hjelpefigur!

Nedenfor vises en mindre rettvinklet trekant som er tegnet inn som du kan bruke for å hjelpe deg å finne et uttrykk for arealet av den store trekanten.

Fasit

\[ \dfrac{3\sqrt{3}}{4} \]

Løsning

Vi lager en hjelpefigur der vi lager en mindre rettvinklet som vi kan bruke til å finne et uttrykk for arealet av den store trekanten som vist til høyre.

Vi trenger å et uttrykk for grunnlinja og høyden til trekanten for å kunne finne et uttrykk for arealet.

Fra Pytagoras’ setning har vi at

\[ \ell^2 + x^2 = 1^2 \]

Vi kan løse denne likningen for $\ell$:

\[ \ell = \sqrt{1 - x^2} \]

Grunnlinjen $g$ til den store trekanten er da $g = 2\ell$.

Høyden til trekanten vil være $h = x + 1$.

Arealet $A$ av trekanten kan da skrives som:

\[ A = \dfrac{g \cdot h}{2} = \dfrac{2\ell \cdot h}{2} = \ell \cdot h \]

Setter vi inn uttrykket for $\ell$ og $h$, får vi funksjonen

\[ A(x) = \ell \cdot h = \sqrt{1 - x^2} \cdot (x + 1) = (x + 1)\sqrt{1 - x^2} \]

For å bestemme det største arealet $A$ vi kan få, så løser vi $A'(x) = 0$ og sjekker at $A''(x) < 0$ i punktet for å sikre at det er et toppunkt. Vi bruker CAS til å utføre selve regningen:

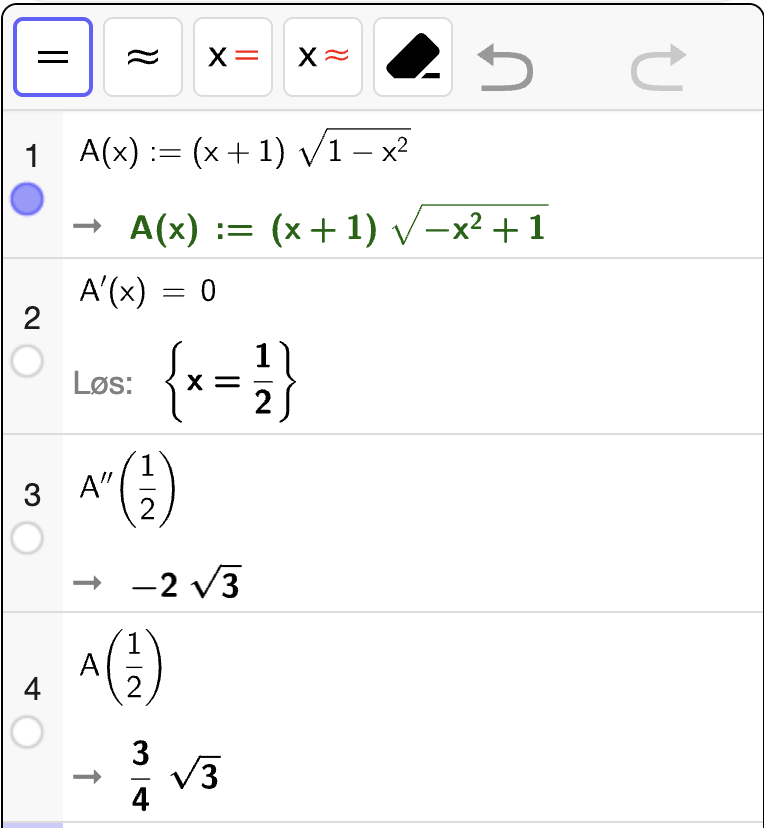
Vi ser at $x = \dfrac{1}{2}$ er et ekstremalpunkt og vi ser at $A''\left(\dfrac{1}{2}\right) < 0$ som betyr at $A$ er konkav frown polynomial icon i nabolaget til punktet. Dermed gir $x = \dfrac{1}{2}$ et toppunkt. Derfor vil arealet $A$ bli størst mulig når $x = \dfrac{1}{2}$. Fra utskriften kan vi da også konkludere at det eksakte største arealet er

\[ A\left(\dfrac{1}{2}\right) = \dfrac{3\sqrt{3}}{4} \]

Oppgave 13

En kjegle med sirkulær grunnflate med radius $r$ og høyde $h$ er innskrevet i en kule med radius $1$.

Se figuren nedenfor.

Bestem det største volumet en slik kjegle kan ha.

Fasit

\[ V_\text{størst} = \dfrac{32}{81}\pi \]

Løsning

Først lager vi en hjelpefigur som beskriver tverrsnittet til figuren:

Volumet av en kjegle er gitt ved

\[ V = \dfrac{Gh}{3} \]

der $G$ er arealet av grunnflaten og $h$ er høyden. Arealet av grunnflaten er gitt ved

\[ G = \pi r^2 \]

Høyden $h$ er gitt ved

\[ h = 1 + \ell \]

Fra figuren kan vi bruke Pytagoras’ setning på den rettvinkla trekanten til å skrive opp sammenhengen:

\[ r^2 + \ell^2 = 1^2 \]

Fra dette finner vi at

\[ \ell = \sqrt{1 - r^2} \]

Det betyr at høyden er

\[ h = 1 + \sqrt{1 - r^2} \]

Dermed vil volumet av kjeglen kunne uttrykkes som en funksjon av $r$:

\[ V(r) = \dfrac{\pi r^2 \left(1 + \sqrt{1 - r^2}\right)}{3} \]

Vi bruker CAS til å bestemme ekstremalpunktene til $V$ og avgjør hvilke av punktene som er toppunkter ved å sjekke at $V''(r) < 0$ i punktet:

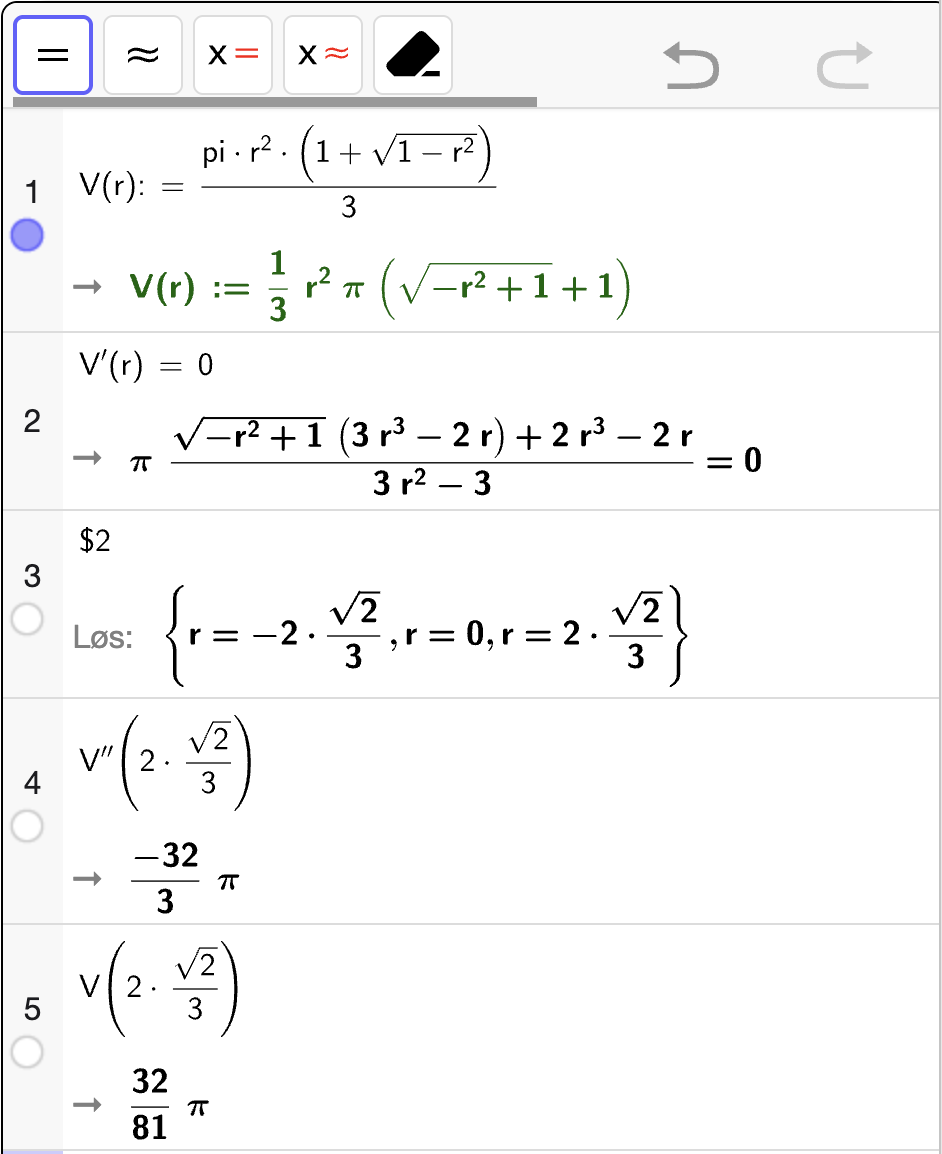
Fra utskriften ser vi at $V'(r) = 0$ når

\[ r = 0 \or r = \pm \dfrac{2\sqrt{2}}{3} \]

Når $r = 0$ så er $V(r) = 0$ så dette er opplagt ikke det største volumet. Den eneste løsningen som gir mening er derfor $r = \dfrac{2\sqrt{2}}{3}$. Vi ser også at $V''\left(\dfrac{2\sqrt{2}}{3}\right) < 0$ som betyr at $V$ er konkav frown polynomial icon i nabolaget til punktet. Dermed gir $r = \dfrac{2\sqrt{2}}{3}$ et toppunkt. Derfor vil volumet $V$ bli størst mulig når $r = \dfrac{2\sqrt{2}}{3}$. Fra utskriften kan vi da også konkludere at det eksakte største volumet er

\[ V_\text{størst} = \dfrac{32}{81}\pi \]