10. Deriverbarhet

Oppgave 1

En funksjon \(f\) er gitt ved

\[\begin{split} f(x) = \begin{cases} x^2 \qfor x < 1 \\ \\ 2x - 1 \qfor x \geq 1 \end{cases} \end{split}\]

Bestem \(f'(1)\) hvis den eksisterer.

Fasit

\[ f'(1) = 2 \]

Løsning

Vi lar \(g(x) = x^2\) og \(h(x) = 2x - 1\). Begge funksjonene er kontinuerlige og deriverbare i \(x = 1\), så vi sjekker bare om \(g(1) = h(1)\) og \(g'(1) = h'(1)\). Først sjekker vi kontinuiteten:

\[ g(1) = 1^2 = 1 \and h(1) = 2 \cdot 1 - 1 = 1 \]

Altså er \(f\) kontinuerlig i \(x = 1\). Nå sjekker vi deriverbarheten:

\[ g'(x) = 2x \limplies g'(1) = 2 \cdot 1 = 2 \]

og

\[ h'(x) = 2 \limplies h'(1) = 2 \]

Altså er \(h'(1) = g'(1)\) så \(f\) er deriverbar i \(x = 1\) og \(f'(1) = 2\).

---

Oppgave 2

En funksjon \(f\) er gitt ved

\[\begin{split} \begin{cases} x^2 + 2 \qfor x < 1 \\ \\ -x^2 + 2x \qfor x \geq 1 \end{cases} \end{split}\]

Bestem \(f'(1)\) hvis den eksisterer.

Fasit

\(f\) er ikke kontinuerlig i \(x = 1\), så \(f'(1)\) eksisterer ikke.

Løsning

Vi lar

\[ g(x) = x^2 + 2 \qog h(x) = -x^2 + 2x \]

Vi sjekker først om \(f\) er kontinuerlig i \(x = 1\) ved å sjekke at \(g(1) = h(1)\). Vi har

\[ g(1) = 1^2 + 2 = 3 \qog h(1) = -1^2 + 2\cdot 1 = -1 + 2 = 1 \]

Altså er \(g(1) \neq h(1)\), så \(f\) er ikke kontinuerlig i \(x = 1\). Men da er ikke \(f\) deriverbar i \(x = 1\) heller.

---

Oppgave 3

En funksjon \(f\) er gitt ved

\[\begin{split} f(x) = \begin{cases} \dfrac{x^3 + 8}{x + 2} \qhvis x \neq -2 \\ \\ a \qhvis x = -2 \end{cases} \end{split}\]

a

Bestem \(a\) slik at \(f\) er kontinuerlig i \(x = -2\).

Fasit

\[ a = 12 \]

Løsning

For å bestemme verdien til \(a\) som gjør at \(f\) er kontinuerlig i \(x = -2\), så må vi bruke definisjonen av kontinuitet:

\[ \lim_{x \to -2} f(x) = f(-2) \]

Vi har at \(f(-2) = a\), så vi må finne grenseverdien \(\lim_{x \to -2} f(x)\). Vi har

\[\begin{split} \begin{align*} \lim_{x \to -2} f(x) &= \lim_{x \to -2} \dfrac{x^3 + 8}{x + 2} \\ \\ &\overset{[\frac{0}{0}]}{=} \lim_{x} \to -2} \dfrac{3x^2}{1} \\ \\ &= 3 \cdot (-2)^2 = 12 \end{align*} \end{split}\]

Altså må \(a = 12\) for at \(f\) skal være kontinuerlig i \(x = -2\).

b

Bestem \(f'(-2)\) hvis den eksisterer.

Fasit

\[ f'(-2) = -6 \]

Løsning

Vi bruker definisjonen av den deriverte til å se om vi kan bestemme en verdi for \(f'(-2)\). Da får vi

\[\begin{split} \begin{align*} f'(-2) &= \lim_{x \to -2} \dfrac{f(x) - f(-2)}{x - (-2)} \\ \\ &= \lim_{x \to -2} \dfrac{\dfrac{x^3 + 8}{x + 2} - 12}{x + 2} \\ \\ &= \lim_{x \to -2} \dfrac{\dfrac{x^3 + 8 - 12(x + 2)}{x + 2}}{x + 2} \\ \\ &= \lim_{x \to -2} \dfrac{x^3 - 12x - 16}{(x + 2)^2} \\ \\ & \overset{[\frac{0}{0}]}{=} \lim_{x \to -2} \dfrac{3x^2 - 12}{2(x + 2)} \\ \\ &\overset{[\frac{0}{0}]}{=} \lim_{x \to -2} \dfrac{6x}{2} \\ \\ &= \dfrac{6 \cdot (-2)}{2} = -6 \end{align*} \end{split}\]

---

Oppgave 4

En funksjon \(f\) er gitt ved

\[\begin{split} f(x) = \begin{cases} \dfrac{x^3 - 27}{x - 3} \qfor x \neq 3 \\ \\ a \qfor x = 3 \end{cases} \end{split}\]

a

Bestem \(a\) slik at \(f\) er kontinuerlig i \(x = 3\).

Fasit

\[ a = 27 \]

Løsning

For å bestemme \(a\), må vi bruke definisjonen av kontinuitet:

\[ \lim_{x \to 3} f(x) = f(3) \]

Vi har at \(f(3) = a\), så vi må finne grenseverdien \(\lim_{x \to 3} f(x)\). Vi har

\[\begin{split} \begin{align*} \lim_{x \to 3} f(x) &= \lim_{x \to 3} \dfrac{x^3 - 27}{x - 3} \\ \\ &\overset{[\frac{0}{0}]}{=} \lim_{x \to 3} \dfrac{3x^2}{1} \\ \\ &= 3 \cdot 3^2 = 27 \end{align*} \end{split}\]

Altså må \(a = 27\) for at \(f\) skal være kontinuerlig i \(x = 3\).

b

Bestem \(f'(3)\) hvis den eksisterer.

Fasit

\[ f'(3) = 9 \]

Løsning

Vi bruker definisjonen av den deriverte til å se om vi kan bestemme en verdi for \(f'(3)\). Da får vi

\[\begin{split} \begin{align*} f'(3) &= \lim_{x \to 3} \dfrac{f(x) - f(3)}{x - 3} \\ \\ &= \lim_{x \to 3} \dfrac{\dfrac{x^3 - 27}{x - 3} - 27}{x - 3} \\ \\ &= \lim_{x \to 3} \dfrac{\dfrac{x^3 - 27 - 27(x - 3)}{x - 3}}{x - 3} \\ \\ &= \lim_{x \to 3} \dfrac{x^3 - 27x + 81}{(x - 3)^2} \\ \\ & \overset{[\frac{0}{0}]}{=} \lim_{x \to 3} \dfrac{3x^2 - 27}{2(x - 3)} \\ \\ &\overset{[\frac{0}{0}]}{=} \lim_{x \to 3} \dfrac{6x}{2} \\ \\ &= \dfrac{6 \cdot 3}{2} = 9 \end{align*} \end{split}\]

---

Oppgave 5

En funksjon \(f\) er gitt ved

\[\begin{split} f(x) = \begin{cases} \dfrac{e^x - 1 - x}{x} \qfor x < 0 \\ \\ a \qfor x = 0 \\ \\ \dfrac{1}{2} \ln (x + 1) \qfor x > 0 \end{cases} \end{split}\]

a

Bestem \(a\) slik at \(f\) er kontinuerlig i \(x = 0\).

Fasit

\[ a = 0 \]

Løsning

Her må vi bruke definisjonen av kontinuitet:

\[ \lim_{x\to 0^-} f(x) = \lim_{x \to 0^+} f(x) = f(0) \]

Vi har at \(f(0) = a\), så vi må bestemme de ensidige grenseverdiene og sjekke at de begge nærmer seg samme verdi.

Vi tar først grenseverdien fra venstre:

\[\begin{split} \begin{align*} \lim_{x \to 0^-} f(x) &= \lim_{x \to 0^-} \dfrac{e^x - 1 - x}{x} \\ \\ &\overset{[\frac{0}{0}]}{=} \lim_{x \to 0^-} \dfrac{e^x - 1}{1} \\ \\ &= e^0 - 1 = 0 \end{align*} \end{split}\]

Så tar vi grenseverdien fra høyre:

\[\begin{split} \begin{align*} \lim_{x \to 0^+} f(x) &= \lim_{x \to 0^+} \dfrac{1}{2} \ln (x + 1) \\ \\ &= \dfrac{1}{2} \ln (0 + 1) = \dfrac{1}{2} \cdot 0 = 0 \end{align*} \end{split}\]

Altså må \(a = 0\) for at \(f\) skal være kontinuerlig i \(x = 0\).

b

Bestem \(f'(0)\) hvis den eksisterer.

Fasit

\[ f'(0) = \dfrac{1}{2} \]

Løsning

Vi bruker definisjonen av den deriverte som sier at

\[ f'(0) = \lim_{x\to 0}\dfrac{f(x) - f(0)}{x - 0} = \lim_{x\to 0}\dfrac{f(x) - f(0)}{x} \]

Vi må ta de ensidige grensene, og hvis disse er like, så vil \(f'(0)\) eksistere.

Vi tar grensen fra venstre først:

\[\begin{split} \begin{align*} f'(0) &= \lim_{x \to 0^-} \dfrac{f(x) - f(0)}{x} \\ \\ &= \lim_{x \to 0^-} \dfrac{\dfrac{e^x - 1 - x}{x} - 0}{x} \\ \\ &= \lim_{x \to 0^-} \dfrac{e^x - 1 - x}{x^2} \\ \\ &\overset{[\frac{0}{0}]}{=} \lim_{x \to 0^-} \dfrac{e^x - 1}{2x} \\ \\ &\overset{[\frac{0}{0}]}{=} \lim_{x \to 0^-} \dfrac{e^x}{2} \\ \\ &= \dfrac{e^0}{2} = \dfrac{1}{2} \end{align*} \end{split}\]

Så tar vi grenseverdien fra høyre:

\[\begin{split} \begin{align*} f'(0) &= \lim_{x \to 0^+} \dfrac{f(x) - f(0)}{x} \\ \\ &= \lim_{x \to 0^+} \dfrac{\dfrac{1}{2} \ln (x + 1) - 0}{x} \\ \\ &= \lim_{x \to 0^+} \dfrac{\ln (x + 1)}{2x} \\ \\ &\overset{[\frac{0}{0}]}{=} \lim_{x \to 0^+} \dfrac{\dfrac{1}{x + 1}}{2} \\ \\ &= \dfrac{1}{2 \cdot (0 + 1)} = \dfrac{1}{2} \end{align*} \end{split}\]

De to grensene er like som betyr at \(f'(0)\) eksisterer og er gitt ved

\[ f'(0) = \dfrac{1}{2} \]

---

Oppgave 6

En funksjon \(f\) er gitt ved

\[\begin{split} f(x) = \begin{cases} e^x - 1 \qfor x < 0 \\ \\ x \ln (x + 1) \qfor x \geq 0 \end{cases} \end{split}\]

Bestem \(f'(0)\) hvis den eksisterer.

Fasit

\(f'(0)\) eksisterer ikke.

Løsning

Vi må først sjekke at \(f\) er kontinuerlig. Begge forskrifter er kontinuerlig og deriverbare i \(x = 0\). La \(g(x) = e^x - 1\) og \(h(x) = x \ln (x + 1)\). Vi sjekker først kontinuiteten. \(f\) vil være kontinuerlig dersom \(g(0) = h(0)\):

\[ g(0) = e^0 - 1 = 0 \qog h(0) = 0 \cdot \ln (0 + 1) = 0 \]

Ergo er \(f\) kontinuerlig i \(x = 0\). Så sjekker vi deriverbarhet. Vi kan prøve oss på å sjekke om

\[ g'(0) = h'(0) \]

Vi har

\[ g'(x) = e^x \limplies g'(0) = e^0 = 1 \]

Så sjekker vi \(h'(0)\). Vi bruker produktregelen:

\[ h'(x) = \ln (x + 1) + \dfrac{x}{x + 1} \limplies h'(0) = \ln (0 + 1) + \dfrac{0}{0 + 1} = 0 \]

Altså er \(g'(0) \neq h'(0)\), så \(f\) er ikke deriverbar i \(x = 0\) og dermed eksisterer ikke \(f'(0)\).

---

Oppgave 7

En funksjon \(f\) er gitt ved

\[\begin{split} f(x) = \begin{cases} \dfrac{x - 4}{\sqrt{x} - 2} \qfor x \neq 4 \qog x \geq 0 \\ \\ a \qfor x = 4 \end{cases} \end{split}\]

a

Bestem \(a\) slik at \(f\) er kontinuerlig i \(x = 4\).

Fasit

\[ a = 4 \]

Løsning

Uttrykket for \(f(x)\) når \(x \neq 4\) er ikke definert i \(x = 4\), så vi er nødt til å bruke definisjonen av kontinuitet:

\[ \lim_{x \to 4} f(x) = f(4) \]

Vi vet at \(f(4) = a\), så vi må finne grenseverdien \(\lim_{x \to 4} f(x)\). Vi har

\[\begin{split} \begin{align*} \lim_{x \to 4} f(x) &= \lim_{x \to 4} \dfrac{x - 4}{\sqrt{x} - 2} \\ \\ &\overset{[\frac{0}{0}]}{=} \lim_{x \to 4} \dfrac{1}{\left(\dfrac{1}{2\sqrt{x}}\right)} \\ \\ \\ &= \lim_{x \to 4} 2 \sqrt{x} \\ \\ &= 2 \sqrt{4} = 4 \end{align*} \end{split}\]

Altså må \(a = 4\) for at \(f\) skal være kontinuerlig i \(x = 4\).

b

Bestem \(f'(4)\) hvis den eksisterer.

Fasit

\[ f'(4) = \dfrac{1}{4} \]

Løsning

Vi bruker definisjonen av den deriverte til å bestemme \(f'(4)\) dersom den finnes:

\[\begin{split} \begin{align*} f'(4) &= \lim_{x \to 4} \dfrac{f(x) - f(4)}{x - 4} \\ \\ &= \lim_{x \to 4} \dfrac{\dfrac{x - 4}{\sqrt{x} - 2} - 4}{x - 4} \\ \\ &= \lim_{x \to 4} \dfrac{\dfrac{x - 4}{\sqrt{x} - 2} - \dfrac{4(\sqrt{x} - 2)}{\sqrt{x} - 2}}{x - 4} \\ \\ &= \lim_{x \to 4} \dfrac{\dfrac{x - 4 - 4\sqrt{x} + 8}{\sqrt{x} - 2}}{x - 4} \\ \\ &= \lim_{x \to 4} \dfrac{\dfrac{x - 4 \sqrt{x} + 4}{\sqrt{x} - 2}}{x - 4} \\ \\ &= \lim_{x \to 4} \dfrac{x - 4\sqrt{x} + 4}{(\sqrt{x} - 2)(x - 4)} \\ \end{align*} \end{split}\]

Herfra blir det enklere ved å innse at

\[ x - 4\sqrt{x} + 4 = (\sqrt{x})^2 - 2 \cdot 2 \cdot \sqrt{x} + 2^2 = (\sqrt{x} - 2)^2 \]

der vi har brukt 2.kvadratsetning. Da får vi

\[ f'(4) = \lim_{x \to 4} \dfrac{(\sqrt{x} - 2)^2}{(\sqrt{x} - 2)(x - 4)} = \lim_{x \to 4} \dfrac{\sqrt{x} - 2}{x - 4} \overset{[\frac{0}{0}]}{=} \lim_{x \to 4} \dfrac{\dfrac{1}{2\sqrt{x}}}{1} = \dfrac{1}{2 \cdot 2} = \dfrac{1}{4} \]

---

Oppgave 8

Åpne CAS‑vindu

En funksjon \(f\) er gitt ved

\[\begin{split} f(x) = \begin{cases} -9x - 15, \quad x \leq -2 \\ \\ g(x), \quad -2 < x < 1 \\ \\ \dfrac{x^2}{2} - x - \dfrac{7}{2}\, , \quad x \geq 1 \end{cases} \end{split}\]

Funksjonen \(f\) er kontinuerlig og deriverbar for alle \(x \in \mathbb{R}\). Funksjonen \(g\) er en tredjegradsfunksjon.

Bestem \(g(x)\).

Fasit

\[ a = -\dfrac{13}{27} \and b = \dfrac{7}{9} \and c = -\dfrac{1}{9} \and d = -\dfrac{113}{27} \]

Løsning

Hver forskrift i uttrykket for \(f(x)\) er polynomer som er kontinuerlige og deriverbare der de møtes. Vi lar

\[ p(x) = -9x - 15 \qog q(x) = \dfrac{x^2}{2} - x - \dfrac{7}{2} \]

\(g\) skal være en tredjegradsfunksjon som kan skrives på formen

\[ g(x) = ax^3 + bx^2 + cx + d \]

Siden \(f\) skal være kontinuerlig og deriverbar overalt, så må \(f\) være kontinuerlig og deriverbar i \(x = -2\) og i \(x = 1\). Funksjonen er ellers kontinuerlig og deriverbar fordi den består av polynomer. For at vi skal oppnå dette, må vi sette

\[ p(-2) = g(-2) \and p'(-2) = g'(-2) \and g(1) = q(1) \and g'(1) = q'(1) \]

Da får vi et likningssystem, så er enklest å løse med CAS:

Det blir ikke pent, men vi får at

\[ a = -\dfrac{13}{27} \and b = \dfrac{7}{9} \and c = -\dfrac{1}{9} \and d = -\dfrac{113}{27} \]

---

Oppgave 9

Åpne CAS‑vindu

En funksjon \(f\) er gitt ved

\[\begin{split} f(x) = \begin{cases} ax + b \qfor x < -2 \\ \\ 2x^3 + 2x^2 - 2x \qfor -2 < x < k \\ \\ c \qfor x \geq k \end{cases} \end{split}\]

der \(a, b, c \in \mathbb{R}\) og \(k > -2\).

a

Avgjør om \(f\) er kontinuerlig i \(x = -2\) dersom \(a = 2\) og \(b = -2\).

Fasit

Nei

b

Bestem \(a\), \(b\), \(c\), og \(k\) slik at \(f\) er kontinuerlig og deriverbar i \(x = -2\) og \(x = k\).

Fasit

Det er to muligheter.

Mulighet 1:

\[ a = 14 \and b = 24 \and c = 2 \and k = -1 \]

Mulighet 2:

\[ a = 14 \and b = 24 \and c = -\dfrac{10}{27} \and k = \dfrac{1}{3} \]

Løsning

Vi lar

\[\begin{split} \begin{align*} p(x) &= ax + b \\ \\ g(x) &= 2x^3 + 2x^2 - 2x \\ \\ h(x) &= c \end{align*} \end{split}\]

For at \(f\) skal være kontinuerlig og deriverbar i \(x = -2\), så må følgende likninger være oppfylt:

\[ p(-2) = g(-2) \and p'(-2) = g'(-2) \]

For at \(f\) skal være kontinuerlig og deriverbar i \(x = k\), så må følgende likninger være oppfylt:

\[ g(k) = h(k) \and g'(k) = h'(k) \]

Dette gir oss et likningssystem som vi kan løse med CAS:

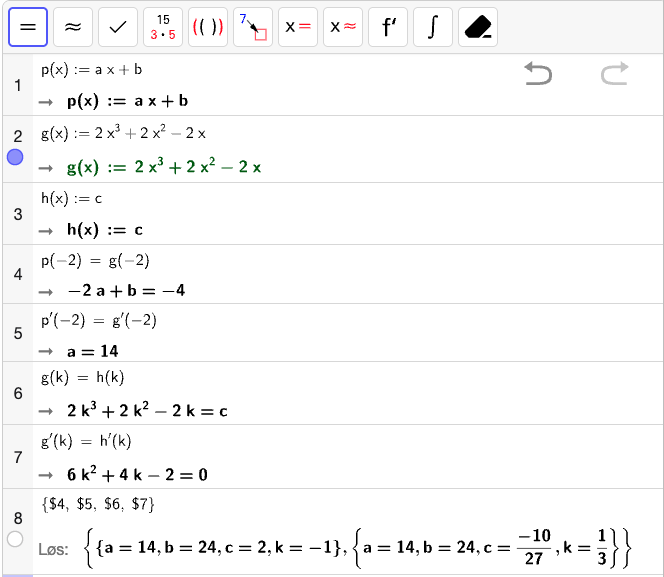
Vi får dermed to mulige løsninger:

\[ a = 14 \and b = 24 \and c = 2 \and k = -1 \]

eller

\[ a = 14 \and b = 24 \and c = -\dfrac{10}{27} \and k = \dfrac{1}{3} \]