Krasjkurs 1#
Læringsmål
Kunne bruke CAS til å regne funksjoner og bestemme funksjonsverdier, den deriverte, ekstremalpunkter og ukjente koeffisienter.
Kunne bruke CAS til å løse likninger, likningssystemer og ulikheter
Kjenne til matematiske funksjoner i CAS som \(\ln x\), \(\log_a (x)\) og \(e^x\).
Funksjoner#
Det er noen matematiske funksjoner i R1 som vi må kunne bruke i CAS. Her er en oversikt over de vi trenger:
Funksjon |
Notasjon i CAS |
Eksempel |
|---|---|---|
\(\ln(x)\) |
|
|
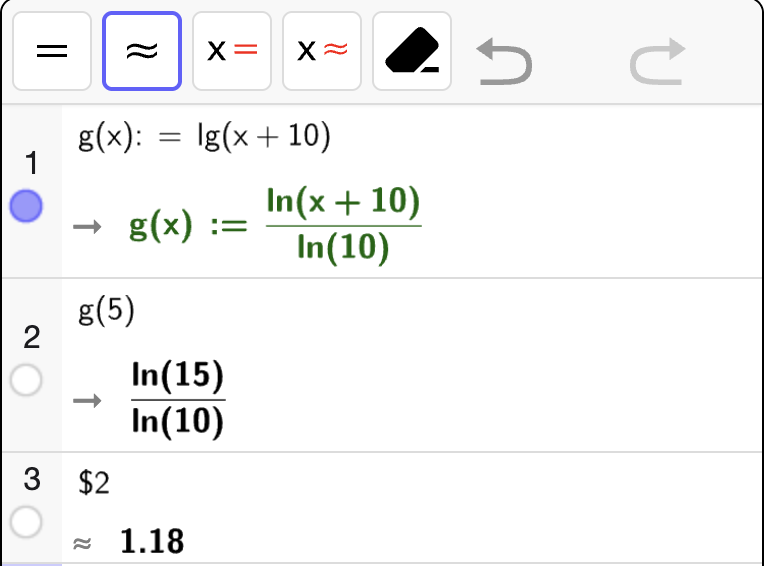
\(\lg(x)\) |
|
|
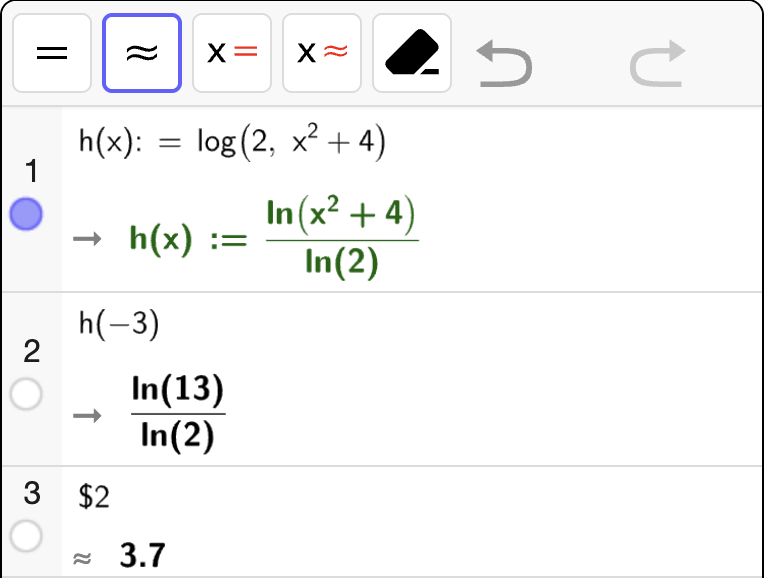
\(\log_a(x)\) |
|
|
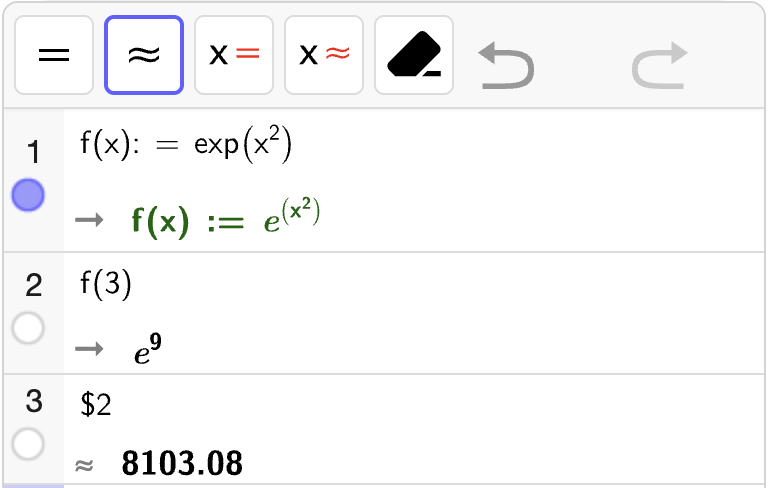
\(e^x\) |
|
|
Funksjonsverdier#
Det er i blant nyttig å kunne regne ut funksjonsverdier \(f(x)\), og det kan gjøres raskt og enkelt med CAS.
Utforsk 1
I gif-en nedenfor regner vi ut \(f(2)\) eksakt og numerisk for funksjonen
Å regne ut eksakte verdier gjør vi med – dette er det vi får som standard ved å bare trykke på enter ⏎. Å regne ut numeriske verdier gjør vi ved å trykke på
.
Bruk CAS-vinduet og følge eksempelet i gif-en.

Fig. 1 Først defineres funksjon \(f(x)\). Det er viktig å bruke := og ikke bare = for at det skal bli en funksjon. Deretter regner vi ut \(f(2)\) både eksakt og numerisk ved å bruke og
.#
Funksjonsverdier til \(f'\) og \(f''\)#
Vi kan også regne ut funksjonsverdier for den deriverte \(f'\), eller den andrederiverte \(f''\) for en gitt funksjon \(f\).
Utforsk 2
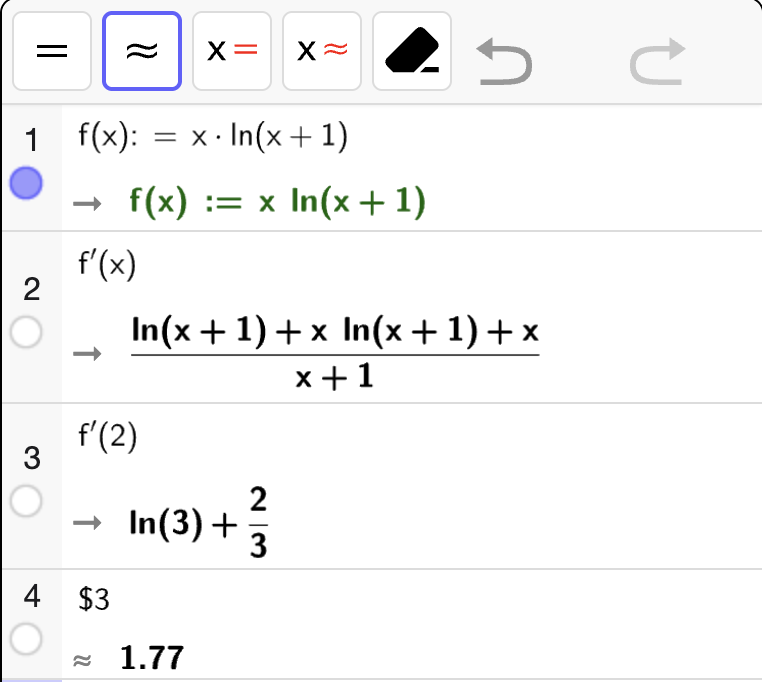
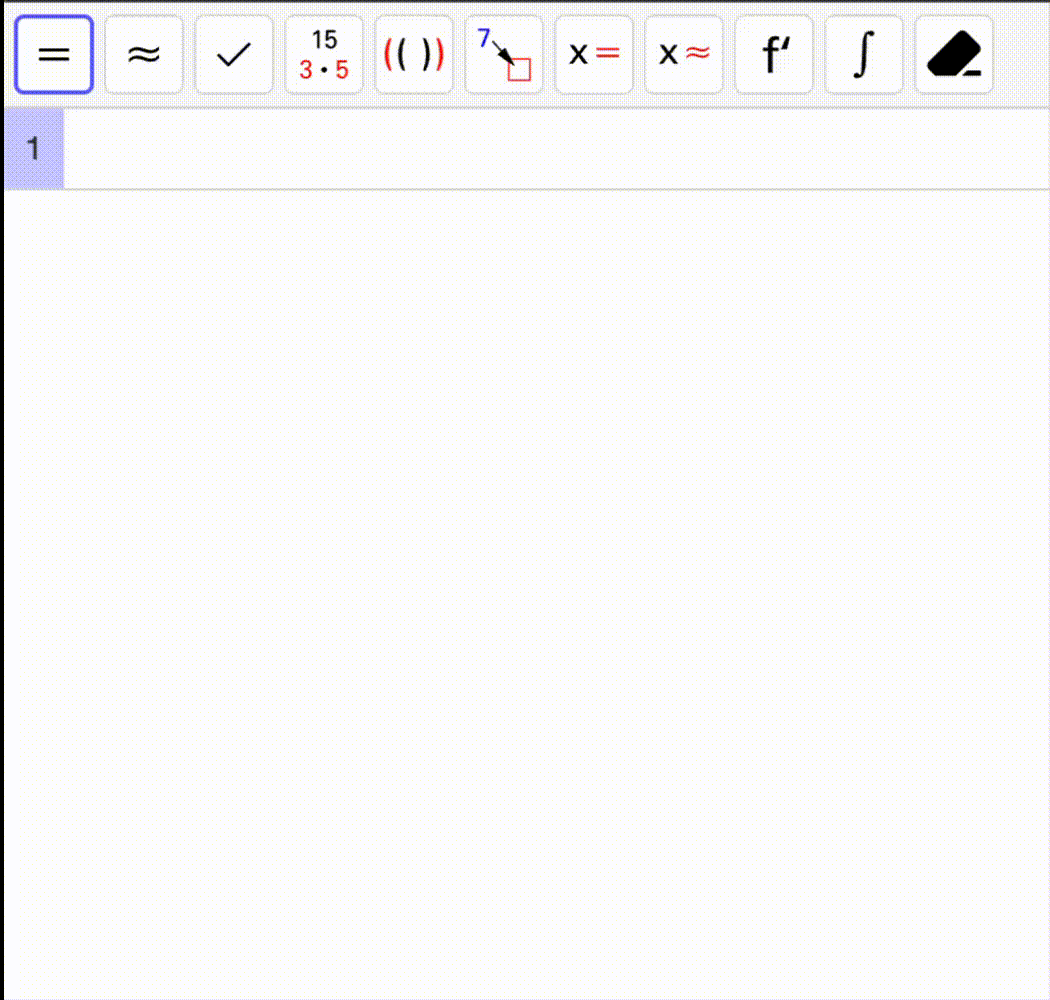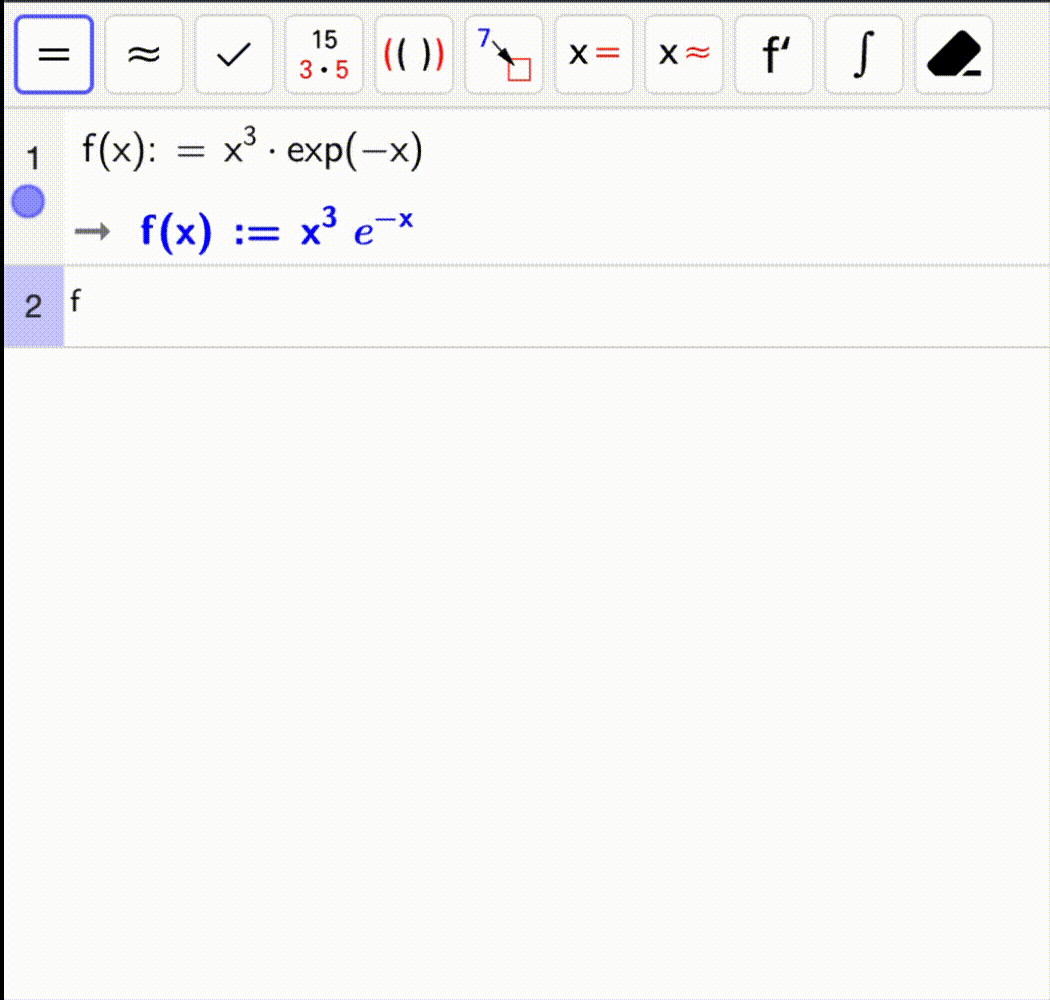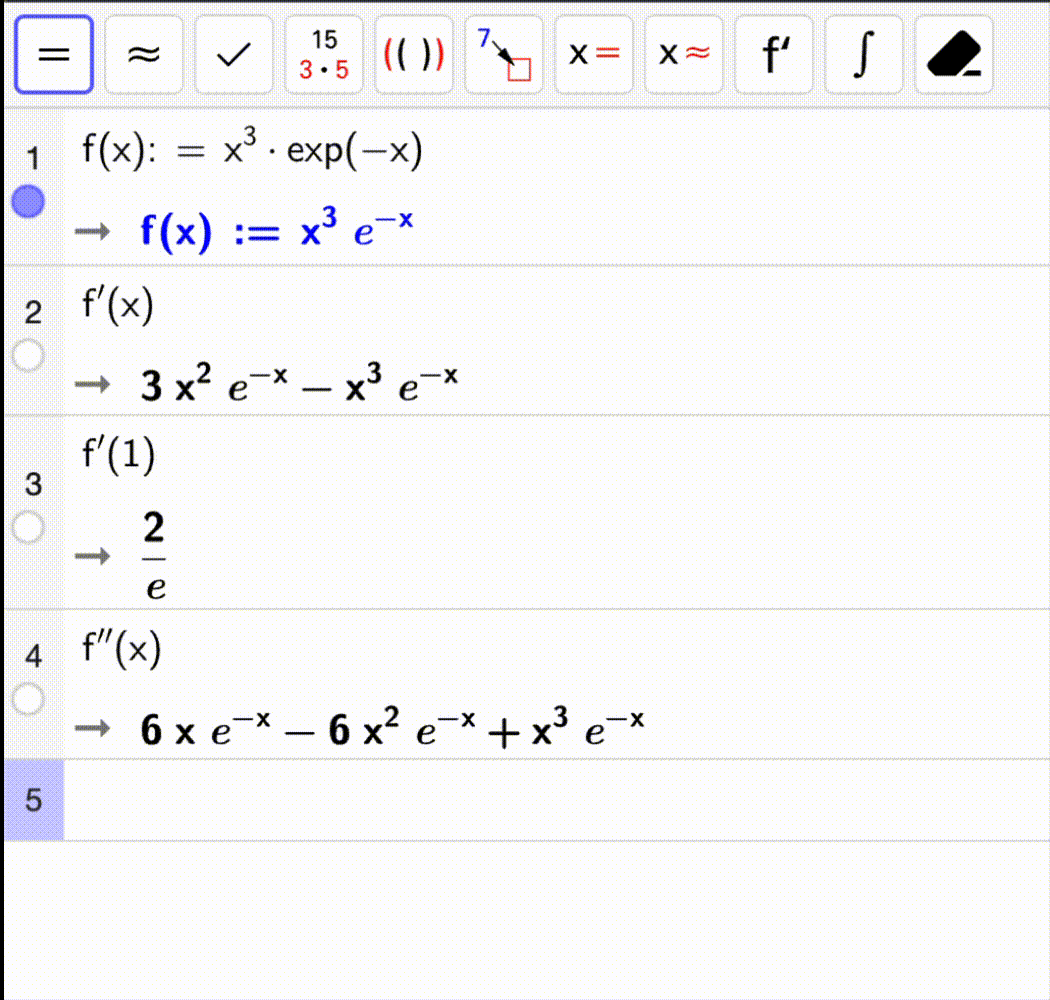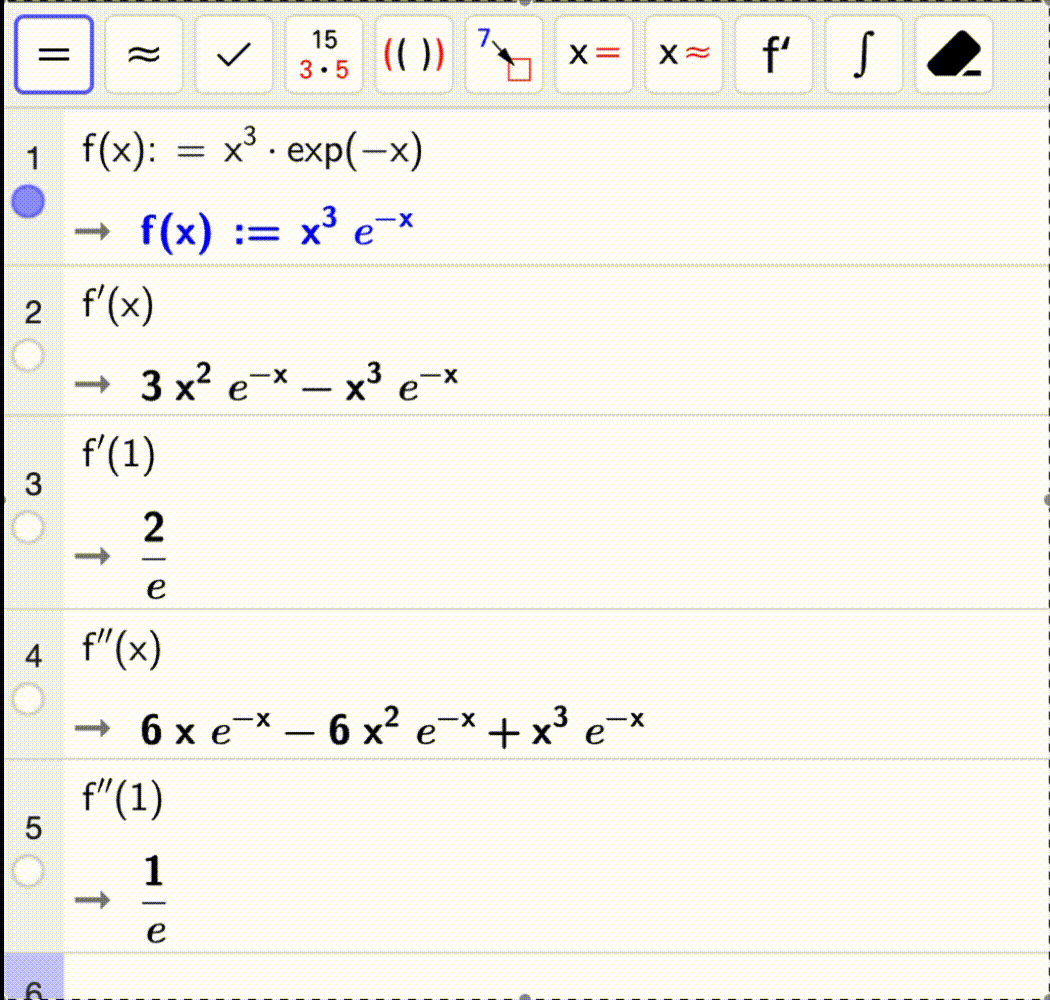
I gif-en nedenfor regner vi ut \(f'(x)\), \(f''(x)\), \(f'(1)\) og \(f''(1)\) for funksjonen
For å få den deriverte skriver vi bare f'(x) og for den andrederiverte f''(x).
Bruk CAS-vinduet og følg eksempelet.
Underveisoppgave 2
En funksjon \(f\) er gitt ved
Bestem \(f'(x)\).
Bestem \(f'(2)\) eksakt og numerisk.
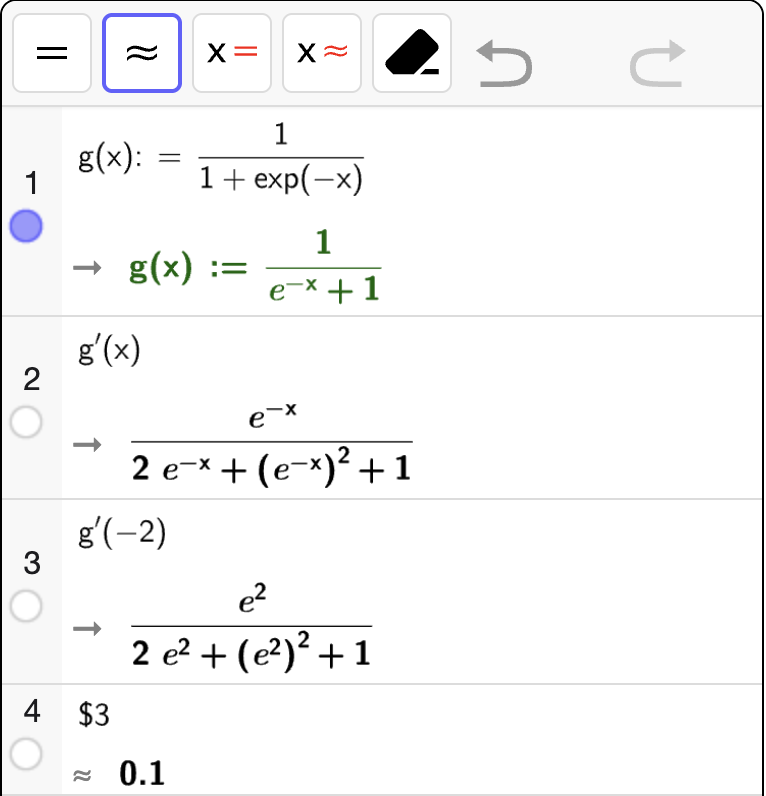
En funksjon \(g\) er gitt ved
Bestem \(g'(x)\).
Bestem \(g'(-2)\) eksakt og numerisk.
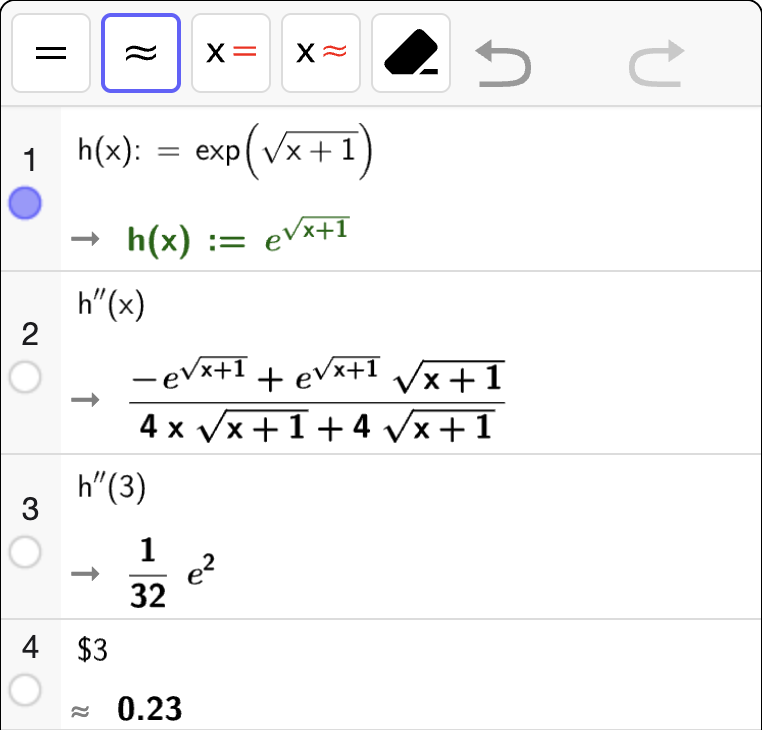
En funksjon \(h\) er gitt ved
Bestem \(h''(x)\)
Bestem \(h''(3)\) eksakt og numerisk.
Bestemme \(f(x)\) med likningssystem#
I en del sammenhenger ønsker vi å bestemme koeffisientene til en funksjon \(f\) gitt ved et funksjonsuttrykk med ukjente koeffisienter, før vi skal bruke funksjonen videre til å løse andre problemstillinger med funksjonen. Dette er det neste vi skal se på.
Utforsk 3
I figuren til høyre vises en andregradsfunksjon
sammen med noen punkter på grafen til \(f\).
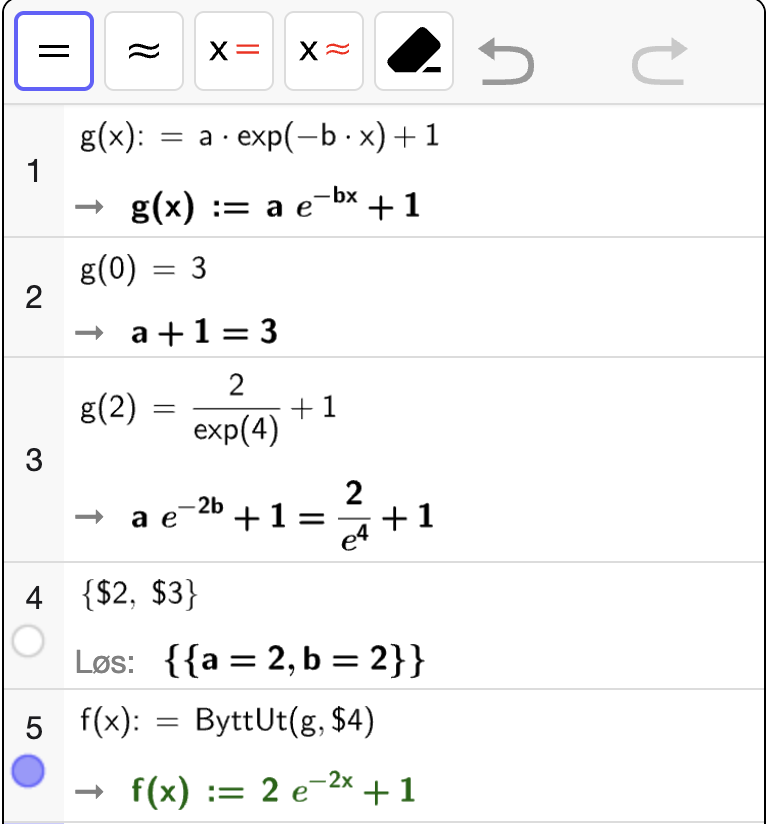
I gif-en nedenfor vises det hvordan man bestemmer koeffisientene \(a\), \(b\) og \(c\) med et likningssystem og setter de inn i \(f(x)\). Oppskriften er:
Lag en testfunksjon \(g(x)\) med de ukjente koeffisientene.
Løs et likningssystem for koeffisientene ved å bruke punktene på grafen til \(f\).
Erstatt koeffisientene i testfunksjonen \(g(x)\) med CAS-funksjonen
ByttUtog definer \(f(x)\) med det nye uttrykket.
Prøv med CAS-vinduet og følg eksempelet i gif-en nedenfor.

Fig. 2 Først definerer vi en testfunksjon \(g(x)\) med de ukjente koeffisientene. Deretter lager vi et likningssystem og løser det med . Til slutt bruker vi
ByttUt(uttrykk, liste med forandringer) til å definere \(f(x)\) med de riktige koeffisientene.#
Underveisoppgave 3
I figuren til høyre vises grafen til en funksjon \(f\) gitt ved
Bestem \(f(x)\).
I figuren til høyre vises grafen til en funksjon \(f\) gitt ved
Bestem \(f(x)\).
Likninger#
De fleste likningene vi jobber med vil være tilknyttet funksjoner. Denne typen problemstillinger egner seg godt for CAS.
Eksakt løsning#
Utforsk 4
I figuren til høyre vises grafen til funksjonen
Vi skal bestemme følgende eksakt:
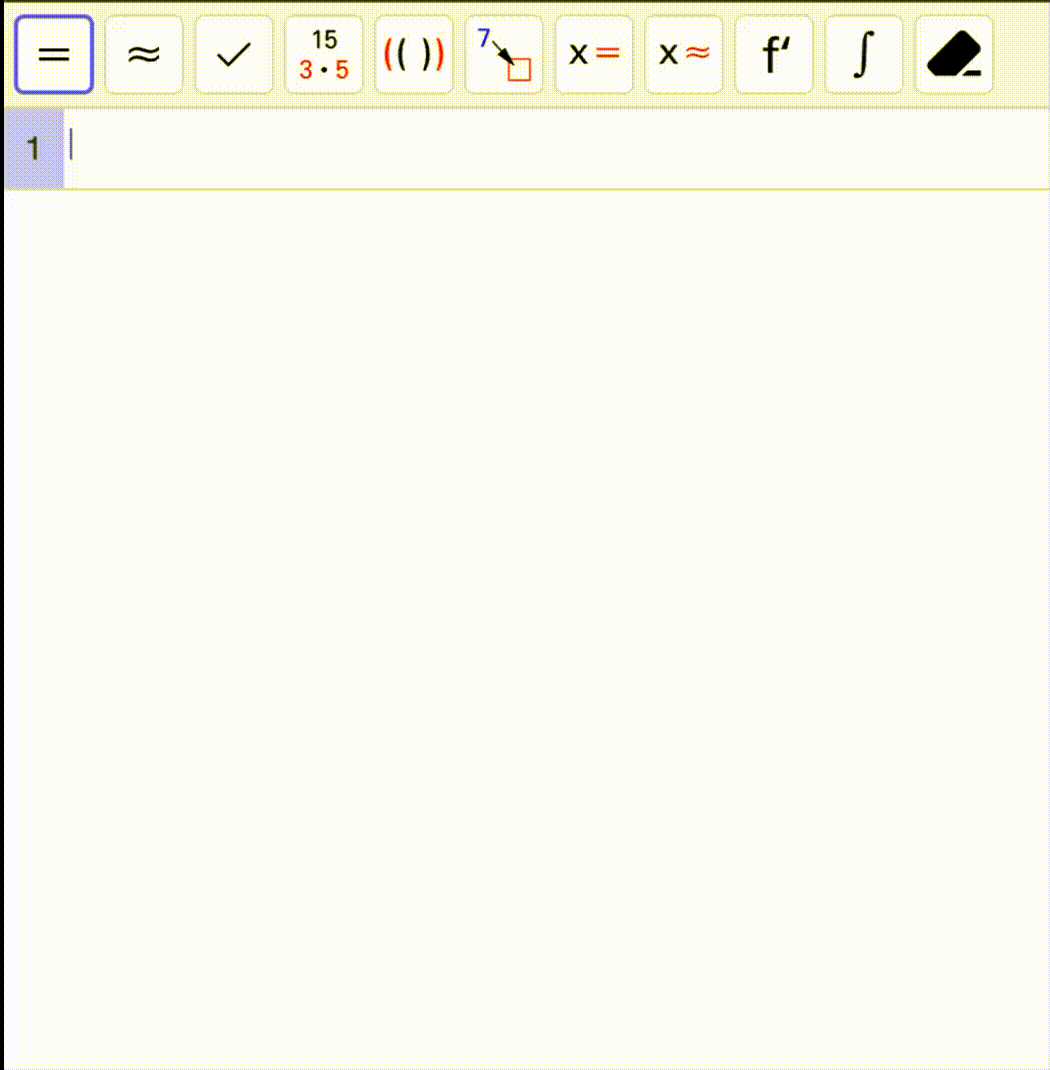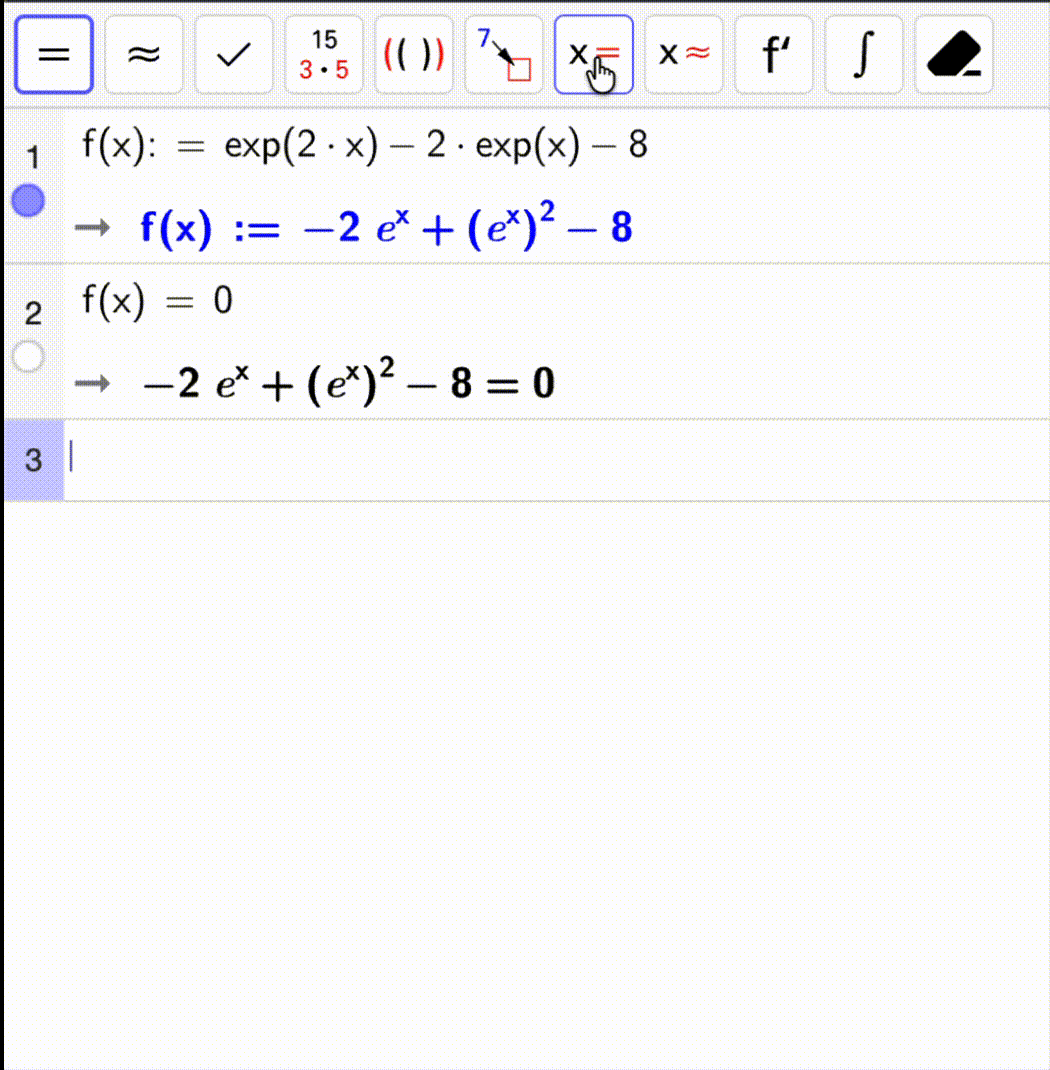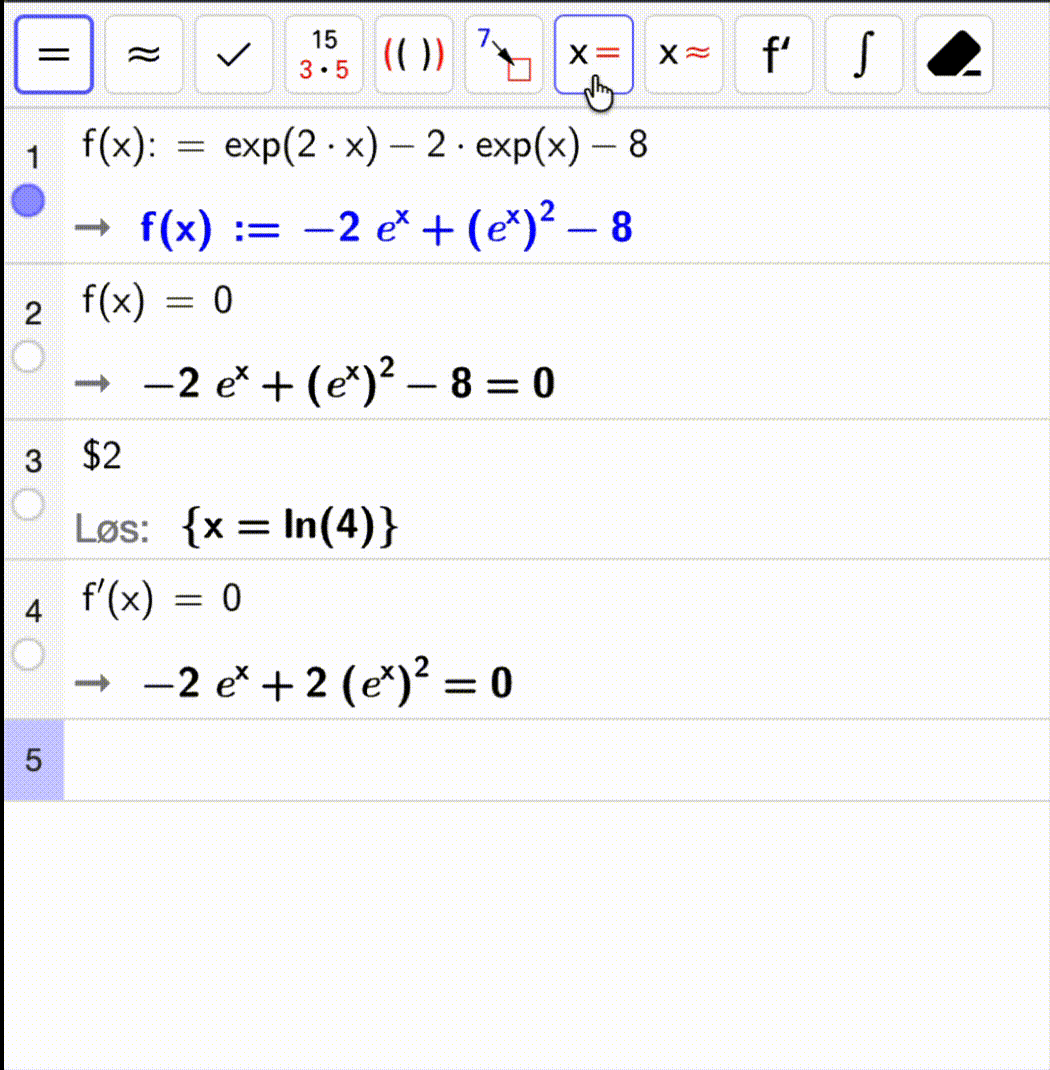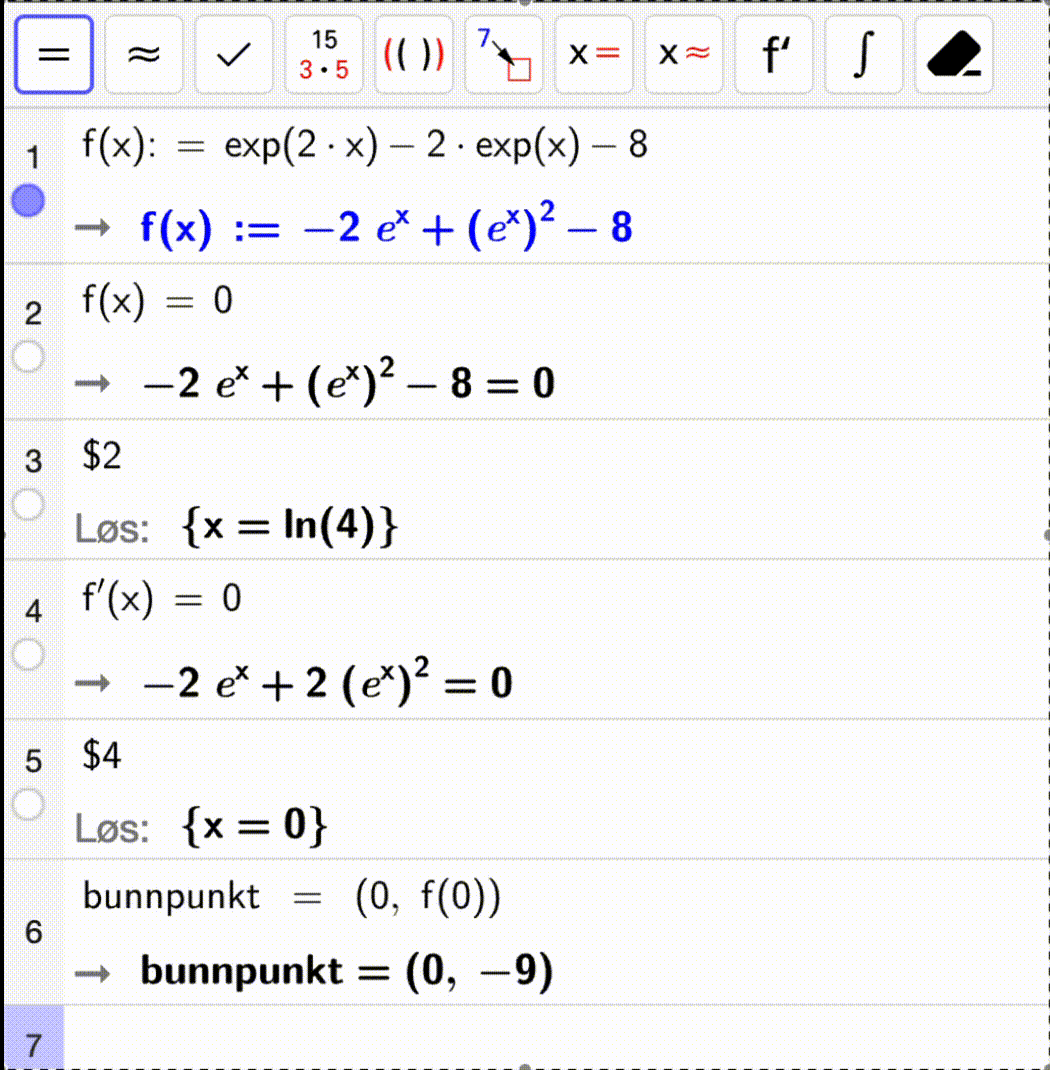
Nullpunktet til \(f\).
Koordinatene til bunnpunktet til \(f\).
Bruk CAS-vinduet og følg løsningen nedenfor – eller prøv selv først og sjekk løsningen etterpå!
Underveisoppgave 4
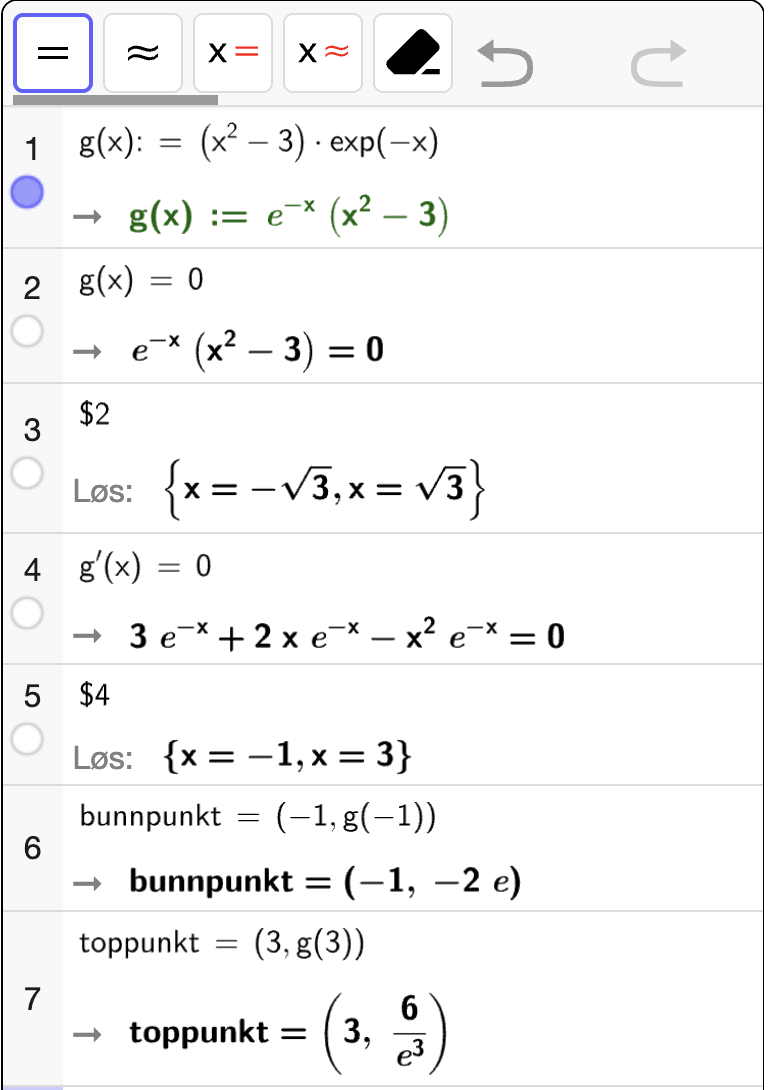
I figuren til høyre vises grafen til
Bestem nullpunktene til \(f\).
Bestem koordinatene til eventuelle topp- og bunnpunkter på grafen til \(f\).
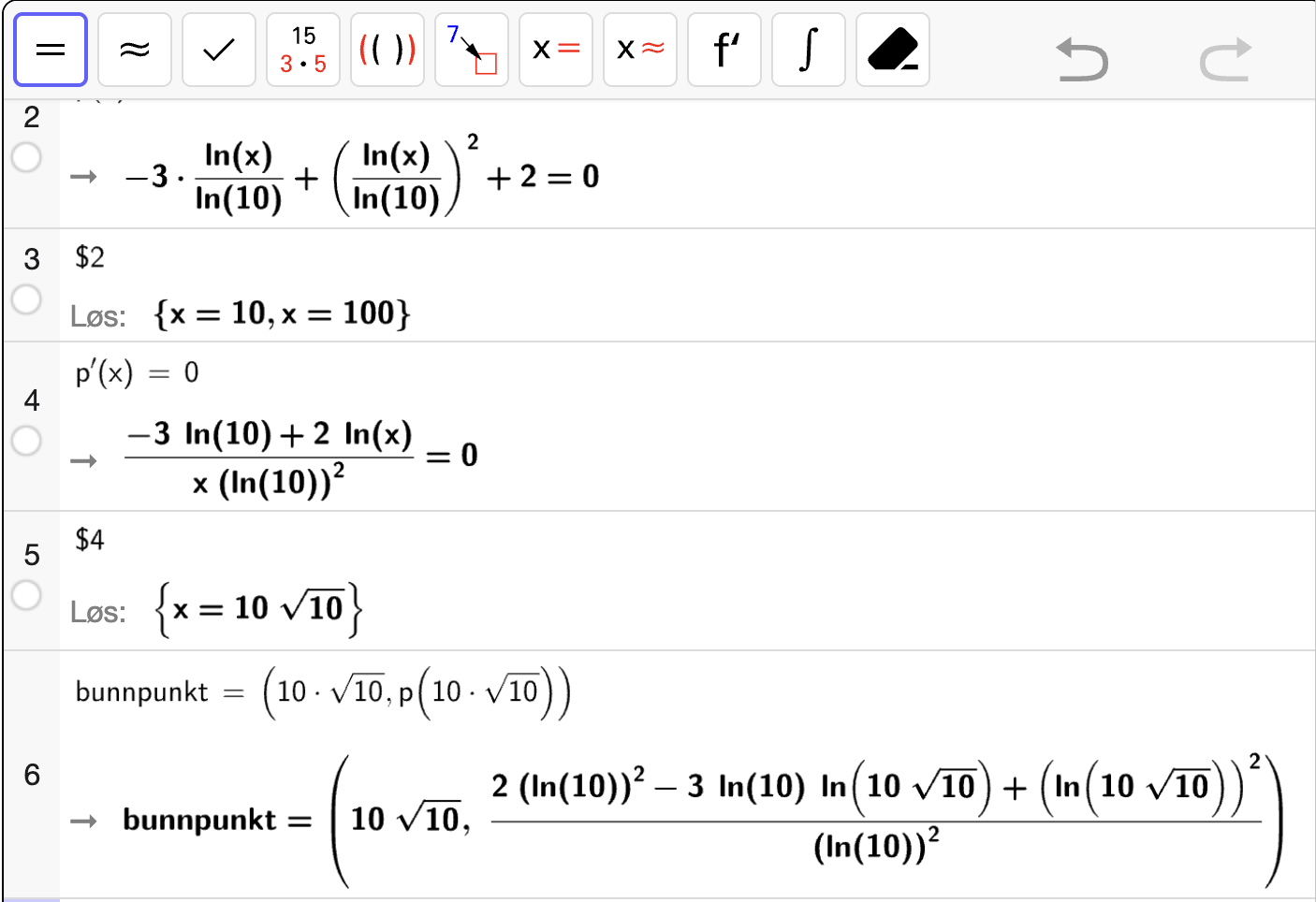
I figuren til høyre vises grafen til
Bestem nullpunktene til \(g\).
Bestem koordinatene til eventuelle topp- og bunnpunkter på grafen til \(g\).
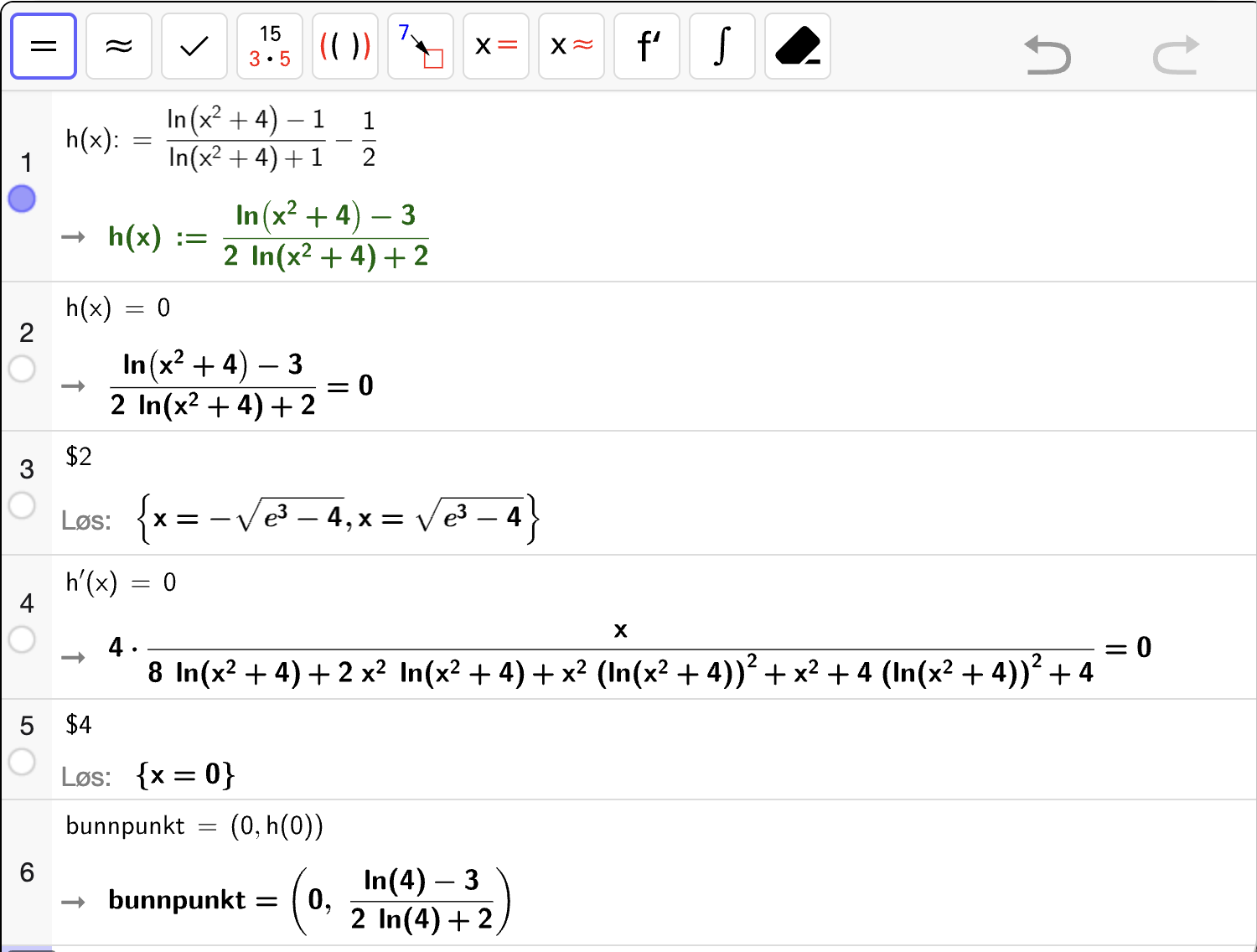
I figuren til høyre vises grafen til
Bestem nullpunktene til \(h\).
Bestem koordinatene til eventuelle topp- og bunnpunkter på grafen til \(h\).
Numerisk løsning#
Med noen likninger, vil det være umulig å få \(x\) alene uansett hvor hardt vi prøver. Da er det numerisk løsning som er vår eneste utvei.
Utforsk 5
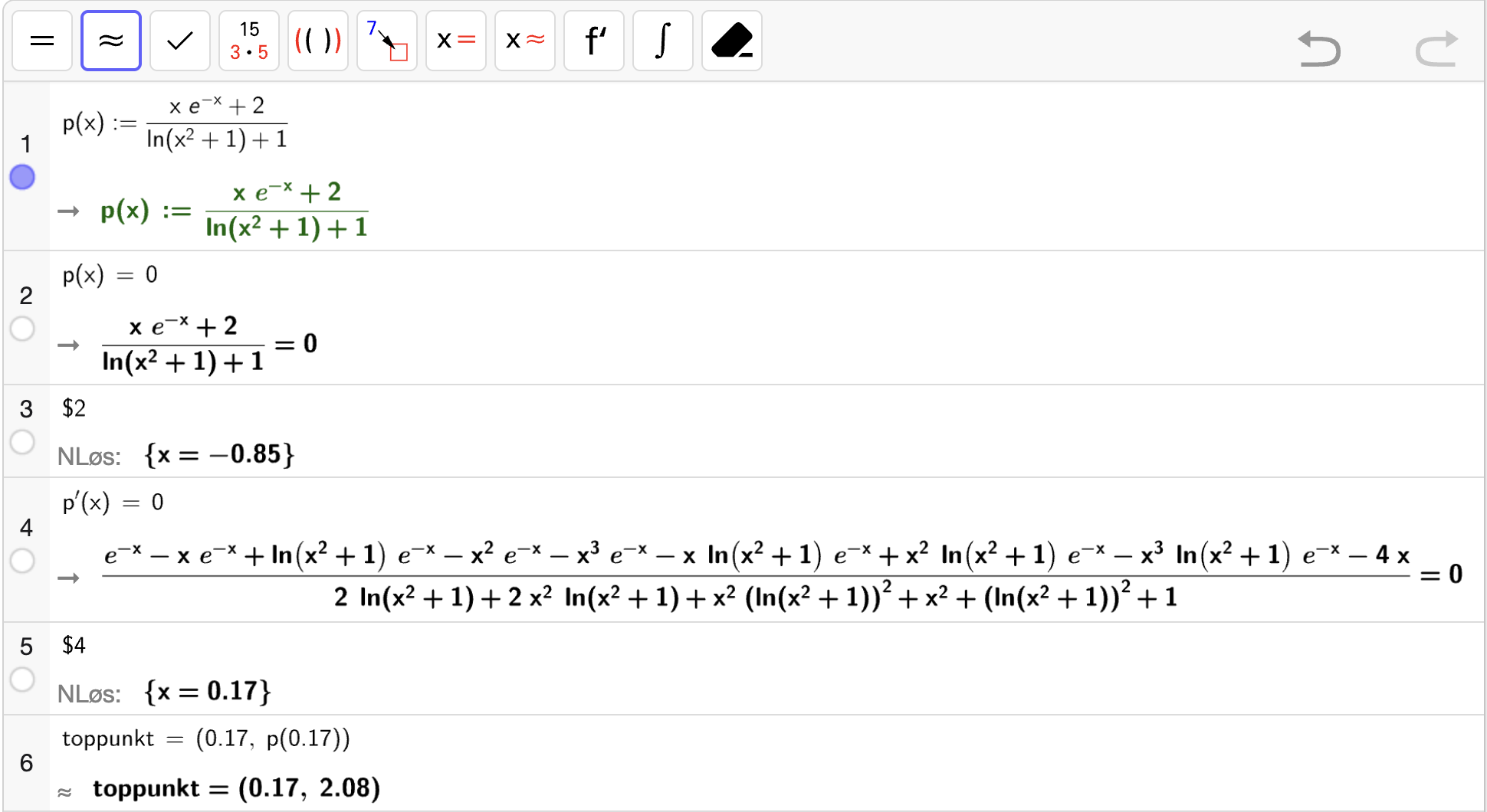
I figuren til høyre vises grafen til
Vi skal bestemme nullpunktet til \(f\).
Bruk CAS-vinduet til å følge løsningen nedenfor.
Underveisoppgave 5
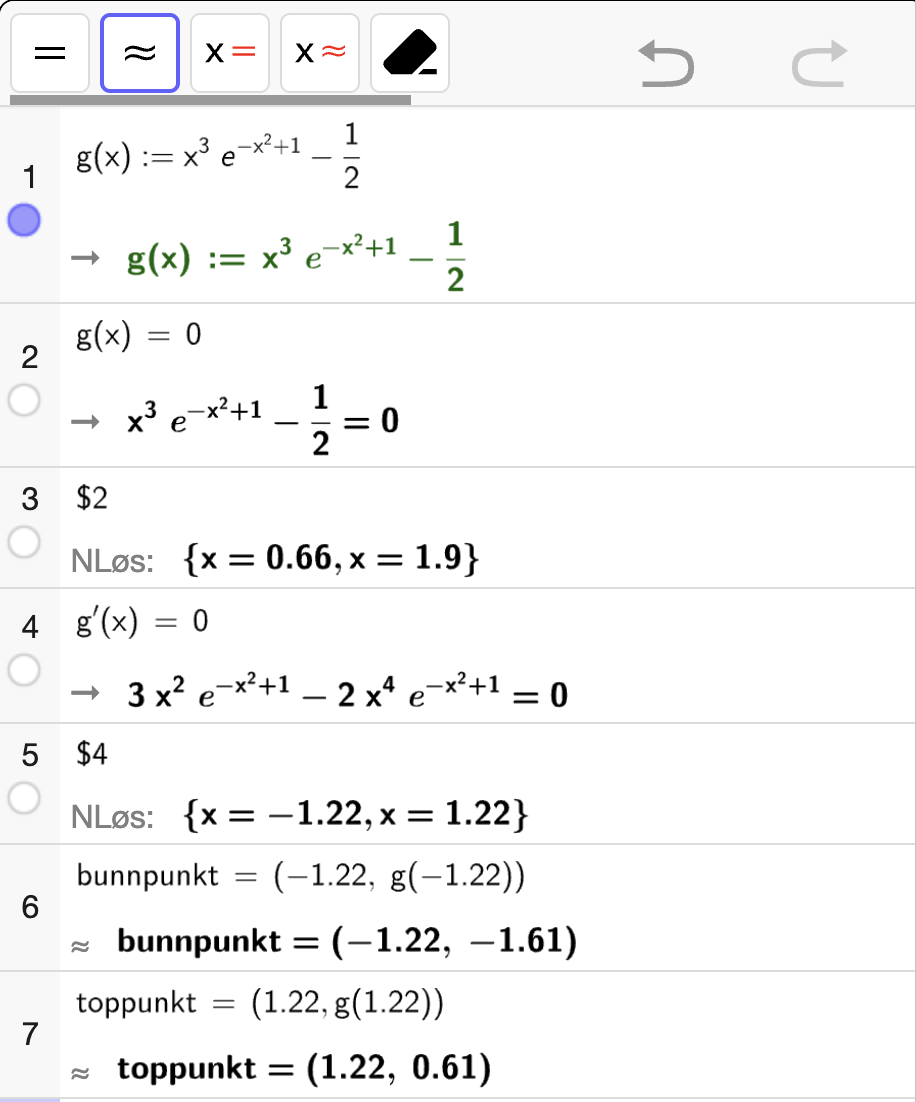
I figuren til høyre vises grafen til
Bestem nullpunktene til \(f\).
Bestem koordinatene til eventuelle topp- og bunnpunkter på grafen til \(f\).
I figuren til høyre vises grafen til
Bestem nullpunktene til \(g\) numerisk.
Bestem koordinatene til eventuelle topp- og bunnpunkter på grafen til \(g\) numerisk.
I figuren til høyre vises grafen til
Bestem nullpunktene til \(h\) numerisk.
Bestem koordinatene til eventuelle topp- og bunnpunkter på grafen til \(h\) numerisk.