Oppgavesamling 1

Oppgavesamling 1#

Oppgaver der en CAS-knapp er vist, kan tenkes på som en “del 2”-oppgave

Oppgave 1

Løs likningene

\[ 3 \cdot 2^x = 4 \cdot 5^{x} \]

Fasit

\[ x = \dfrac{\ln 4 - \ln 3}{\ln 2 - \ln 5} \]

Løsning

\[ 3 \cdot 2^x = 4 \cdot 5^x \]
\[ \ln (3 \cdot 2^x) = \ln (4 \cdot 5^x) \]
\[ \ln 3 + \ln 2^x = \ln 4 + \ln 5^x \]
\[ \ln 3 + x \cdot \ln 2 = \ln 4 + x \cdot \ln 5 \]
\[ x \ln 2 - x \ln 5 = \ln 4 - \ln 3 \]
\[ x\left(\ln 2 - \ln 5\right) = \ln 4 - \ln 3 \]
\[ x = \dfrac{\ln 4 - \ln 3}{\ln 2 - \ln 5} \]
\[ e^{2x} - e^x - 6 = 0 \]

Fasit

\[ x = \ln 3 \]

Løsning

Vi gjør variabelskifte \(u = e^x\) slik at likningen kan skrives om til

\[ u^2 - u - 6 = 0 \]

Så løser vi likningen for \(u\) med \(abc\)-formelen:

\[ u = \dfrac{1 \pm \sqrt{(-1)^2 - 4 \cdot 1 \cdot (-6)}}{2 \cdot 1} = \dfrac{1 \pm \sqrt{25}}{2} = \dfrac{1 \pm 5}{2} \]
\[ u = -2 \or u = 3 \]

Da får vi

\[ e^x = -2 \or e^x = 3 \]

Den første av de likningene har ingen løsningen siden vi ikke kan opphøye \(e\) med noe som gir et negativt tall. Dermed får vi bare

\[ e^x = 3 \liff x = \ln 3 \]
\[ \lg (x - 3) + \lg x = 1 \]

Fasit

\[ x = 5 \]

Løsning

\[ \lg (x - 3) + \lg x = 1 \]
\[ \lg \left((x - 3) \cdot x\right) = 1 \]
\[ \lg (x^2 - 3x) = 1 \]
\[ x^2 - 3x = 10^1 \]
\[ x^2 - 3x - 10 = 0 \]
\[ x = \dfrac{3 \pm \sqrt{(-3)^2 - 4 \cdot 1 \cdot (-10)}}{2 \cdot 1} = \dfrac{3 \pm \sqrt{49}}{2} = \dfrac{3 \pm 7}{2} \]
\[ x = -2 \or x = 5 \]

Vi må forkaste \(x = -2\), fordi vi ikke kan ta logaritmen av et negativt tall – noe vi ville gjort i den opprinnelige likningen hvis vi satt i \(x = -2\). Dermed får vi bare

\[ x = 5 \]
\[ (\lg x)^2 + 3 \lg x - 4 = 0 \]

Fasit

\[ x = 10^{-4} \or x = 10^1 \]

Løsning

Vi gjør variabelskifte \(u = \lg x\) slik at vi får andregradslikningen

\[ u^2 + 3u - 4 = 0 \]

Så løser vi likningen for \(u\) med \(abc\)-formelen:

\[ u = \dfrac{-3 \pm \sqrt{3^2 - 4 \cdot 1 \cdot (-4)}}{2 \cdot 1} = \dfrac{-3 \pm \sqrt{25}}{2} = \dfrac{-3 \pm 5}{2} \]
\[ u = -4 \or u = 1 \]

Dermed får vi at

\[ \lg x = -4 \or \lg x = 1 \]

som gir

\[ x = 10^{-4} \or x = 10 \]

Oppgave 2

Bestem grenseverdiene

\[ \lim_{x \to 2} \dfrac{x - 2}{x^3 - 8} \]

Fasit

\[ \lim_{x \to 2} \dfrac{x - 2}{x^3 - 8} = \dfrac{1}{12} \]

Løsning

\[ \begin{align*} \lim_{x \to 2} \dfrac{x - 2}{x^3 - 8} & \overset{[\frac{0}{0}]}{=} \lim_{x \to 2} \dfrac{1}{3x^2} = \dfrac{1}{3 \cdot 2^2} = \dfrac{1}{12} \end{align*} \]
\[ \lim_{x \to \infty} \dfrac{3x^2 + 4x + 1}{2x^2 - x + 5} \]

Fasit

\[ \lim_{x \to \infty} \dfrac{3x^2 + 4x + 1}{2x^2 - x + 5} = \dfrac{3}{2} \]

Løsning

\[ \begin{align*} \lim_{x \to \infty} \dfrac{3x^2 + 4x + 1}{2x^2 - x + 5} & \overset{[\frac{\infty}{\infty}]}{=} \lim_{x \to \infty} \dfrac{6x + 4}{4x - 1} \overset{[\frac{\infty}{\infty}]}{=} \lim_{x \to \infty} \dfrac{6}{4} = \dfrac{3}{2} \end{align*} \]
\[ \lim_{x \to 0} \dfrac{e^x - e^{-x}}{x} \]

Fasit

\[ \lim_{x \to 0} \dfrac{e^x - e^{-x}}{x} = 2 \]

Løsning

\[ \begin{align*} \lim_{x \to 0} \dfrac{e^x - e^{-x}}{x} & \overset{[\frac{0}{0}]}{=} \lim_{x \to 0} \dfrac{e^x + e^{-x}}{1} = e^0 + e^0 = 2 \end{align*} \]
\[ \lim_{x \to 1} \dfrac{\ln x}{x - 1} \]

Fasit

\[ \lim_{x \to 1} \dfrac{\ln x}{x - 1} = 1 \]

Løsning

\[ \begin{align*} \lim_{x \to 1} \dfrac{\ln x}{x - 1} & \overset{[\frac{0}{0}]}{=} \lim_{x \to 1} \dfrac{\frac{1}{x}}{1} = \dfrac{1}{1} = 1 \end{align*} \]

Oppgave 3

En funksjon \(f\) er gitt ved

\[\begin{split} f(x) = \begin{cases} x^2 - 4 & \qhvis x < 2 \\ \\ ax + b & \qhvis x \geq 2 \end{cases} \end{split}\]

Bestem \(a\) og \(b\) slik at \(f\) er kontinuerlig og deriverbar i \(x = 2\).

Fasit

\[ a = 4 \and b = -8 \]

Løsning

Vi lar \(g(x) = x^2 - 4\) og \(h(x) = ax + b\). Da er \(f(x) = g(x)\) når \(x < 2\) og \(f(x) = h(x)\) når \(x \geq 2\). For at \(f\) skal være kontinuerlig i \(x = 2\), må vi ha at

\[ g(2) = h(2) \liff 2^2 - 4 = a \cdot 2 + b \liff 0 = 2a + b \]

For at \(f\) skal være deriverbar i \(x = 2\), må vi ha at

\[ g'(2) = h'(2) \liff 2 \cdot 2 = a \liff 4 = a \]

Setter vi inn \(a = 4\) i den første likningen, får vi

\[ 0 = 2 \cdot 4 + b \liff b = -8 \]

Altså er \(f\) kontinuerlig og deriverbar i \(x = 2\) når

\[ a = 4 \and b = -8 \]

Oppgave 4

Deriver funksjonene

\[ f(x) = e^{4x} + \ln 3x + \pi \]

Fasit

\[ f'(x) = 4e^{4x} + \dfrac{1}{x} \]

Løsning

\[\begin{split} \begin{align*} f'(x) &= \left(e^{4x} + \ln 3x + \pi \right)' \\ \\ &= (e^{4x})' + (\ln 3x)' + (\pi)' \\ \\ &= 4e^{4x} + \dfrac{1}{x} \end{align*} \end{split}\]
\[ g(x) = x e^{-2x} \]

Fasit

\[ g'(x) = (1 - 2x)e^{-2x} \]

Løsning

\[\begin{split} \begin{align*} g'(x) &= \left(x e^{-2x}\right)' \\ \\ &= (x)' \cdot e^{-2x} + x \cdot (e^{-2x})' \\ \\ &= 1 \cdot e^{-2x} + x \cdot (-2e^{-2x}) \\ \\ &= e^{-2x} - 2xe^{-2x} \\ \\ &= (1 - 2x)e^{-2x} \end{align*} \end{split}\]
\[ h(x) = \dfrac{\ln x}{x} \]

Fasit

\[ h'(x) = \dfrac{1 - \ln x}{x^2} \]

Løsning

\[\begin{split} \begin{align*} h'(x) &= \left(\dfrac{\ln x}{x}\right)' \\ \\ &= \dfrac{(\ln x)' \cdot x - \ln x \cdot (x)'}{x^2} \\ \\ &= \dfrac{\dfrac{1}{x} \cdot x - \ln x \cdot 1}{x^2} \\ \\ &= \dfrac{1 - \ln x}{x^2} \end{align*} \end{split}\]
\[ p(x) = \sqrt{\ln x} \]

Fasit

\[ p'(x) = \dfrac{1}{2x\sqrt{\ln x}} \]

Løsning

\[\begin{split} \begin{align*} p'(x) &= \left(\sqrt{\ln x}\right)' \\ \\ &= \dfrac{1}{2\sqrt{\ln x}} \cdot (\ln x)' \\ \\ &= \dfrac{1}{2\sqrt{\ln x}} \cdot \dfrac{1}{x} \\ \\ &= \dfrac{1}{2x\sqrt{\ln x}} \end{align*} \end{split}\]

Oppgave 5

En funksjon \(f\) er gitt ved

\[ f(x) = (x + 1)e^{-x} \]

Bestem eventuelle nullpunkter for \(f\).

Fasit

\[ x = -1 \]

Løsning

For å bestemme eventuelle nullpunkter for \(f\), så løser vi likningen \(f(x) = 0\):

\[ f(x) = 0 \liff (x + 1)e^{-x} = 0 \]

Da får vi at

\[ x + 1 = 0 \or e^{-x} = 0 \]

Den andre likningen har ingen løsning, siden \(e^{-x}\) aldri er lik null. Dermed får vi bare

\[ x + 1 = 0 \liff x = -1 \]

Bestem koordinatene til eventuelle topp- og bunnpunkter på grafen til \(f\).

Husk å begrunne om punktene er topp- eller bunnpunkter.

Fasit

Toppunkt i \((0, 1)\).

Løsning

For å bestemme eventuelle topp- og bunnpunkter på grafen til \(f\), løser vi \(f'(x) = 0\).

Først deriverer vi:

\[\begin{split} \begin{align*} f'(x) &= \left((x + 1)e^{-x}\right)' \\ \\ &= (x + 1)' \cdot e^{-x} + (x + 1) \cdot (e^{-x})' \\ \\ &= 1 \cdot e^{-x} + (x + 1) \cdot (-e^{-x}) \\ \\ &= e^{-x} - (x + 1)e^{-x} \\ \\ &= (1 - (x + 1))e^{-x} \\ \\ &= -x e^{-x} \end{align*} \end{split}\]

Så løser vi likningen \(f'(x) = 0\):

\[ f'(x) = 0 \liff -x e^{-x} = 0 \]

Det gir oss at

\[ x = 0 \or e^{-x} = 0 \]

Den andre likningen har ingen løsning, siden \(e^{-x}\) aldri er lik null. Dermed får vi bare

\[ x = 0 \]

For å avgjøre om det er et toppunkt eller bunnpunkt, kan vi tegne en fortegnslinje for \(f'(x)\):

2026-01-26T15:53:30.180720 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/

Her er \(e^x\) vist som en av faktorene i fortegnsskjema ovenfor, så skyldes at \(e^{-x} = \dfrac{1}{e^x}\)

Altså stiger grafen før \(x = 0\) og synker etter. Dermed har vi et toppunkt i \(x = 0\). For å finne \(y\)-verdien, setter vi inn i \(f\):

\[ f(0) = (0 + 1)e^{0} = 1 \]

Altså har grafen til \(f\) et toppunkt i \((0, 1)\).

Oppgave 6

En funksjon \(f\) er gitt ved

\[ f(x) = e^{-2x} + \dfrac{1}{5}x^5 - 2\pi \]

Bestem likningen for tangenten til grafen til \(f\) i punktet \((0, f(0))\).

Fasit

\[ y = -2x + 1 - 2\pi \]

Løsning

Likningen til tangenten er gitt ved

\[ y = f(0) + f'(0)\cdot (x - 0) = f(0) + f'(0) \cdot x. \]

Vi har at

\[ f(0) = e^{-2\cdot 0} + \dfrac{1}{5}\cdot 0^5 - 2\pi = 1 + 0 - 2\pi 1 - 2\pi \]

Så deriverer vi for å bestemme \(f'(0)\). Da har vi

\[\begin{split} \begin{align*} f'(x) &= \left(e^{-2x} + \dfrac{1}{5}x^5 - 2\pi\right)' \\ \\ &= (e^{-2x})' + \left(\dfrac{1}{5}x^5\right)' - (2\pi)' \\ \\ &= -2e^{-2x} + \dfrac{1}{5}\cdot 5 x^4 - 0 \\ \\ &= -2e^{-2x} + x^4 \end{align*} \end{split}\]

Så regner vi ut \(f'(0)\):

\[ f'(0) = -2e^{-2\cdot 0} + 0^4 = -2 \cdot 1 + 0 = -2 \]

Dermed er likningen til tangenten gitt ved

\[ y = f(0) + f'(0)x = 1 - 2\pi - 2x = -2x + 1 - 2\pi \]

En funksjon \(g\) er gitt ved

\[ g(x) = xe^{-x} + 1 \]

Bestem likningen for tangenten til grafen til \(g\) i \((2, g(2))\).

Fasit

\[ y = -\dfrac{1}{e^2}x + \dfrac{4}{e^2} + 1 \]

En funksjon \(h\) er gitt ved

\[ h(x) = \ln (x^2 + e^2) \]

Bestem liknngen til tangenten til grafen til \(h\) i punktet \((e, h(e))\).

Fasit

\[ y = \dfrac{1}{e}x + \ln 2 + 1 \]

Oppgave 7

En influensaepidemi bryter ut på en videregående skole med 1000 elever. I starten er det få smittede, men antallet øker raskt. Antallet smittede elever \(S(t)\) etter \(t\) dager er tilnærmet gitt ved

\[ S(t) = \dfrac{300}{1 + 28 \cdot e^{-0.3t}} \]

Hvor lang tid tar det før 100 elever er smittet?

Fasit

Det tar omtrent 9 dager før 100 elever er smittet.

Løsning

For å avgjøre hvor lang tid det tar før 100 elever er smittet, så kan vi løse likningen

\[ S(t) = 100 \]

Vi bruker CAS til å løse likningen:

../../../_images/a5.png

Altså vil det ta omtrent \(9\) dager før 100 elever er smittet.

På hvilket tidspunkt blir flest smittet?

Omtrent hvor mange elever blir smittet den dagen?

Fasit

  • Flest blir smittet etter ca. 11 dager.

  • På den dagen blir omtrent 23 elever smittet.

Løsning

For å avgjøre når flest blir smittet, så må vi vite når “stigningen” til grafen er størst. Det vil være i vendepunktet til grafen til \(S\), så vi kan bestemme ved å løse likningen

\[ S''(t) = 0 \]

Vi gjør det med CAS og får:

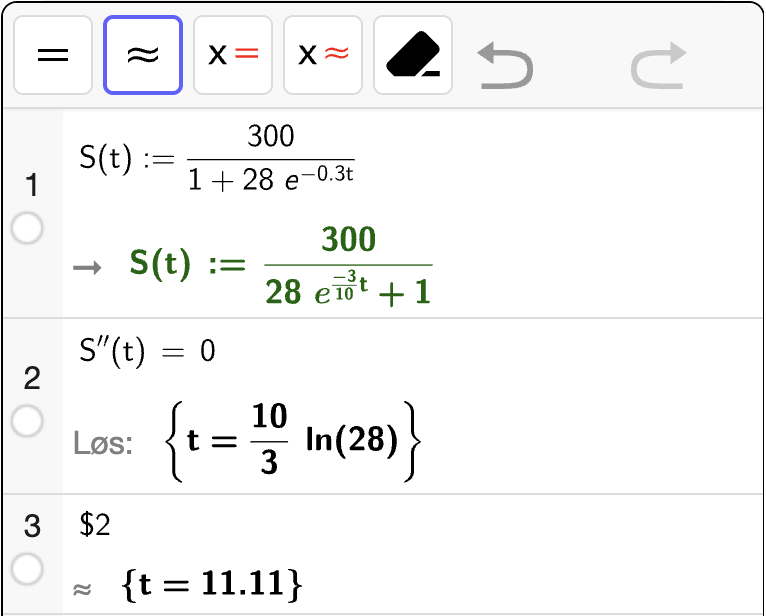
../../../_images/b_1.png

Altså vil flest elever bli smittet etter omtrent \(11\) dager.

For å finne omtrent hvor mange elever som blir smittet på dette tidspunktet, så regner vi ut \(S'(t)\) på dette tidspunktet (siden det gir oss “stigningen” eller da antall som smittes per dag – på den dagen):

../../../_images/b_2.png

Altså får vi at omtrent \(23\) elever smittes den dagen.

Undersøk om \(S\) har asymptoter, og forklar hvilken praktisk tolkning asymptotene eventuelt har.

Løsning

For å undersøke om \(S\) har noen asymptoter, er det enklest å merke seg at

\[ \lim_{t \to \infty} e^{-0.3 t} = 0 \and \lim_{t \to -\infty} e^{-0.3 t} = \infty \]

Da får vi at

\[ \lim_{t \to \infty} S(t) = \lim_{t \to \infty} \dfrac{300}{1 + 28 \cdot e^{-0.3t}} = \dfrac{300}{1 + 28 \cdot 0} = 300 \]

og

\[ \lim_{t \to -\infty} S(t) = \lim_{t \to -\infty} \dfrac{300}{1 + 28 \cdot e^{-0.3t}} = \dfrac{300}{1 + 28 \cdot \infty} = 0 \]

Den første grenseverdien forteller oss at maksimalt 300 elever kan bli smittet i løpet av epidemien, mens den andre grenseverdien forteller oss at ingen var smittet lenge før epidemien startet.

Funksjonen vil ellers ikke ha noen vertikale asymptoter fordi vi ikke kan få nevneren til å bli null på noe vis.

Oppgave 8

En funksjon \(f\) er gitt ved

\[ f(x) = \dfrac{1}{2}e^x (2x - 1)^2 \]

Bestem eventuelle nullpunkter til \(f\).

Fasit

\[ x = \dfrac{1}{2} \]

Vis at

\[ f'(x) = \dfrac{1}{2}e^x (2x - 1)(2x + 3) \]

Bestem koordinatene til eventuelle topp- og bunnpunkter på grafen til \(f\).

Fasit

  • Toppunkt i \(\left(-\dfrac{3}{2}, \dfrac{8}{\sqrt{e^3}}\right)\)

  • Bunnpunkt i \(\left(\dfrac{1}{2}, 0\right)\)

Oppgave 9

En funksjon \(f\) er gitt ved

\[ f(x) = (1 - x^2) e^x \]

Hvilken figur nedenfor viser grafen til \(f\)?

2025-12-06T17:27:57.432668 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/

Fasit

Graf D.

Løsning

Vi kan se at grafene har ulik oppførsel når \(x\to \infty\) og når \(x \to -\infty\). Derfor kan det være hensiktsmessig å sjekke disse grensene først:

\[ \lim_{x \to \infty} f(x) = \lim_{x \to \infty} (1 - x^2)e^x = -\infty \]

Det er bare graf D som går mot \(-\infty\) når \(x \to \infty\). Dermed må graf D vise grafen til \(f\).

Oppgave 10

Anna og Bjørn ser på eksponentiallikningen

\[ 2^x = a \]

Nedenfor vises løsningene til Anna og Bjørn for å bestemme \(x\):

Annas løsning

\[ 2^x = a \]
\[ \log_2 2^x = \log_2 a \]
\[ x = \log_2 a \]

Bjørns løsning

\[ 2^x = a \]
\[ \ln 2^x = \ln a \]
\[ x \ln 2 = \ln a \]
\[ x = \dfrac{\ln a}{\ln 2} \]

Bruk løsningene til Anna og Bjørn til å finne en sammenheng mellom \(\ln a\) og \(\log_2 a\).

Fasit

\[ \log_2 a = \dfrac{\ln a}{\ln 2} \]

Løsning

Siden løsningen til likningen kan skrives på to måter:

\[ x = \log_2 a \and x = \dfrac{\ln a}{\ln 2} \]

så må det bety at

\[ \log_2 a = \dfrac{\ln a}{\ln 2} \]

Oppgave 11

En funksjon \(f\) er gitt ved

\[ f(x) = \log_2 x + 8 \]

Bestem \(f'(x)\).

Hint

Tenk på sammenhengen mellom \(\log_2 x\) og \(\ln x\) som du fant i oppgave 10 og bruk denne til å bestemme \(f'(x)\).

Fasit

\[ f'(x) = \dfrac{1}{x \ln 2} \]

Løsning

Fra oppgave 8 vet vi at

\[ \log_2 x = \dfrac{\ln x}{\ln 2} \]

Dermed har vi at

\[ f(x) = \log_2 x + 8 = \dfrac{\ln x}{\ln 2} + 8 \]

Deriverer vi dette, får vi

\[\begin{split} \begin{align*} f'(x) &= \left(\dfrac{\ln x}{\ln 2} + 8\right)' \\ \\ &= \dfrac{1}{\ln 2} \cdot (\ln x)' + (8)' \\ \\ &= \dfrac{1}{\ln 2} \cdot \dfrac{1}{x} + 0 \\ \\ &= \dfrac{1}{x \ln 2} \end{align*} \end{split}\]

Bestem likningen for tangenten til grafen til \(f\) i punktet \((4, f(4))\).

Fasit

\[ y = \dfrac{1}{4 \ln 2} \left(x - 4\right) + 10 \]

Løsning

Likningen for tangenten i et punkt \(a\) vil være

\[ y = f'(a)\cdot (x - a) + f(a) \]

Her er \(a = 4\), så vi får

\[ y = f'(4) \cdot (x - 4) + f(4) \]

Vi har at

\[ f(4) = \log_2 4 + 8 = 2 + 8 = 10 \]

og

\[ f'(4) = \dfrac{1}{4 \ln 2} \]

Dermed blir likningen til tangenten

\[ y = f'(4) \cdot (x - 4) + f(4) = \dfrac{1}{4 \ln 2} \left(x - 4\right) + 10 \]

Oppgave 12

2026-01-10T13:39:23.171317 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/

Grafen til en funksjon \(f\) er vist i figuren til høyre.

Nedenfor vises fire alternativer om egenskaper ved grafen til \(f\). Kun én av de stemmer – hvilken?

Alternativ 1

\[\begin{split} \begin{align*} \lim_{x \to 1^+} f(x) &= \infty \\ \\ \lim_{x \to -\infty} \left(f(x) - x\right) &= 5 \end{align*} \end{split}\]

Alternativ 2

\[\begin{split} \begin{align*} \lim_{x \to 1^-} f(x) &= -\infty \\ \\ \lim_{x \to \infty} \left(f(x) + x\right) &= 5 \\ \end{align*} \end{split}\]

Alternativ 3

\[\begin{split} \begin{align*} \lim_{x \to 1^+} f(x) &= \infty \\ \\ \lim_{x \to \infty} \left(f(x) - (x - 5)\right) &= 0 \\ \end{align*} \end{split}\]

Alternativ 4

\[\begin{split} \begin{align*} \lim_{x \to 1^-} f(x) &= -\infty \\ \\ \lim_{x \to \infty} \left(f(x) - x\right) &= 5 \\ \end{align*} \end{split}\]

Fasit

Alternativ 2

Løsning

Hvis en linje \(y = ax + b\) er en skrå asymptote for en funksjon \(f\), så må

\[ \lim_{x \to \pm \infty} \left(f(x) - (ax + b)\right) = 0 \]

Alternativ 2 viser denne betingelsen skrevet på en litt annen måte, men vi kan skrive den om:

\[ \lim_{x \to \infty} \left(f(x) + x\right) = 5 \]
\[ \lim_{x \to \infty} \left(f(x) + x - 5\right) = 0 \]
\[ \lim_{x \to \infty} \left(f(x) - (-x + 5)\right) = 0 \]

Altså er linjen \(y = -x + 5\) en skrå asymptote. Dette passer med figuren. I tillegg skal \(f(x) \to -\infty\) når \(x \to 1^-\), som også stemmer med figuren. Dermed er alternativ 2 riktig.

Én av figurene nedenfor viser grafen til \(f'\). Bestem hvilken.

2026-01-10T13:39:23.211308 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/
2026-01-10T13:39:23.248812 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/
2026-01-10T13:39:23.288262 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/
2026-01-10T13:39:23.322734 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/

Fasit

Graf C.

Løsning

Grafen til \(f\) synker før den vertikale asymptoten og stiger etter. Det betyr at den deriverte må være negativ før og positiv etter. I tillegg så må \(f'(x) \to -1\) når \(x\to \pm\infty\) siden dette var stigningstallet til den skrå asymptoten. Disse kriteriene er oppfylt av graf C.

Oppgave 13

En funksjon \(f\) er gitt ved

\[ f(x) = \dfrac{2x - 3}{e^x} \]

Bestem i hvilke punkter grafen til \(f\) skjærer \(x\)-aksen.

Fasit

\[ x = \frac{3}{2} \]

Løsning

\[ f(x) = 0 \liff 2x - 3 = 0 \liff x = \dfrac{3}{2} \]

Bestem koordinatene til eventuelle topp- og bunnpunkter på grafen til \(f\).

Fasit

Toppunkt i \(\left(\dfrac{5}{2}, \dfrac{2}{e^{5/2}}\right)\)

Løsning

Vi må løse \(f'(x) = 0\) for å se etter kandidater for topp- og bunnpunkter. Vi deriverer først:

\[\begin{split} \begin{align*} f'(x) &= \left(\dfrac{2x - 3}{e^x}\right)' = \left((2x - 3)e^{-x}\right)' \\ \\ &= (2x - 3)' \cdot e^{-x} + (2x - 3) \cdot (e^{-x})' \\ \\ &= 2 \cdot e^{-x} + (2x - 3) \cdot (-e^{-x}) \\ \\ &= 2e^{-x} - (2x - 3)e^{-x} \\ \\ &= (2 - (2x - 3))e^{-x} \\ \\ &= (5 - 2x)e^{-x} \end{align*} \end{split}\]

Så løser vi likningen \(f'(x) = 0\):

\[ 5 - 2x = 0 \liff 2x = 5 \liff x = \dfrac{5}{2} \]

For å avgjøre om dette er et topp- eller bunnpunkt, kan vi tegne en fortegnslinje for \(f'(x)\):

2026-01-26T15:53:30.261196 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/

Fra fortegnslinja til \(f'(x)\) ser vi at grafen til \(f\) først stiger og deretter synker etter punktet, som betyr at \(x = \dfrac{5}{2}\) gir et toppunkt. For å finne \(y\)-verdien, setter vi inn i \(f\):

\[ f\left(\dfrac{5}{2}\right) = \dfrac{2 \cdot \dfrac{5}{2} - 3}{e^{5/2}} = \dfrac{5 - 3}{e^{5/2}} = \dfrac{2}{e^{5/2}} \]

Altså har grafen til \(f\) et toppunkt i \(\left(\dfrac{5}{2}, \dfrac{2}{e^{5/2}}\right)\).

Oppgave 14

Anna har skrevet programmet nedenfor.

Bestem en eksakt verdi for verdien programmet skriver ut når det kjøres.

Kjør programmet og sjekk svaret ditt.

Fasit

Programmet skriver ut en numerisk tilnærming til

\[ f'(2) = -\dfrac{1}{2} \]

Løsning

Programmet finner en tilnærming til \(f'(2)\) som vi kan se fra linje 7 der det står

dfdx = (f(x + h) - f(x)) / h

og fra linje 4 og 5 der x = 2 og h = 1e-6 er definert. Funksjonen \(f\) er gitt ved

\[ f(x) = \sqrt{20 - x^2} \]

Så vi bestemmer \(f'(x)\) først og deretter regner ut \(f'(2)\).

\[\begin{split} \begin{align*} f'(x) &= \left(\sqrt{20 - x^2}\right)' \\ \\ &= \dfrac{1}{2\sqrt{20 - x^2}} \cdot (20 - x^2)' \\ \\ &= \dfrac{1}{2\sqrt{20 - x^2}} \cdot (-2x) \\ \\ &= \dfrac{-2x}{2\sqrt{20 - x^2}} \\ \\ &= \dfrac{-x}{\sqrt{20 - x^2}} \end{align*} \end{split}\]

Så setter vi inn \(x = 2\):

\[\begin{split} \begin{align*} f'(2) &= \dfrac{-2}{\sqrt{20 - 2^2}} \\ \\ &= \dfrac{-2}{\sqrt{20 - 4}} \\ \\ &= \dfrac{-2}{\sqrt{16}} \\ \\ &= \dfrac{-2}{4} \\ \\ &= -\dfrac{1}{2} \end{align*} \end{split}\]

Altså vil programmet skrive ut en tilnærming til

\[ f'(2) = -\dfrac{1}{2} \]

Oppgave 15

En funksjon \(f\) er gitt ved

\[ f(x) = e^{x} + 3e^{-x} - 4 \]

Hvilken graf nedenfor viser grafen til \(f\)?

2025-12-06T17:27:57.625349 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/

Fasit

Graf B.

Løsning

Vi kan se at det som skiller grafene er hva som skjer med \(y\)-verdien når \(x \to -\infty\). Vi undersøker derfor denne grensen:

\[ \lim_{x \to -\infty} f(x) = \lim_{x \to -\infty} \left(e^{x} + 3e^{-x} - 4\right) = 0 + \infty - 4 = \infty \]

Altså går \(f(x) \to \infty\) når \(x \to -\infty\). Dette skjer bare for graf B. Dermed må graf B vise grafen til \(f\).

Oppgave 16

Antall rotter som har forvillet seg inn i Jul i Vinterland kan antas å følge en modell på formen

\[ R(x) = \dfrac{500}{1 + ae^{-bx}} \]

der \(a\) og \(b\) er konstanter, og \(x\) er antall dager etter 1. desember. Vi antar at det var 20 rotter den 1. desember og at antall rotter etter 5 dager vil være 100.

Bestem \(a\) og \(b\).

Fasit

\[ a = 24 \and b = \dfrac{1}{5} \ln 6 \]

Bestem \(R'(5)\) og gi en praktisk tolkning av svaret.

Fasit

\[ R'(5) \approx 28.67 \]

som betyr at det kom omtrent 29 nye rotter til Jul i Vinterland i løpet av dag 5.

Hvilken dag i desember vil det komme flest rotter til Jul i Vinterland? Hvor mange rotter kom inn til Jul i Vinterland den dagen?

Fasit

Etter ca. 9 dager, så den 10.desember. Da kom det ca. 45 rotter til Jul i Vinterland.

Hvor mange rotter vil kan det maksimalt bli, ifølge modellen?

Fasit

500

Oppgave 17

I figuren nedenfor vises grafen til en funksjon \(f\) som er gitt ved

\[ f(x) = a (\log_2 x - b) (\log_2 x - c) \qder b < c \]

Bestem \(a\), \(b\) og \(c\).

2026-01-10T13:39:23.408912 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/

Fasit

\[ a = 3 \and b = 1 \and c = 2 \]

Løsning

Vi har at \(f(2) = 0\) og \(f(4) = 0\). Vi har også at

\[ f(x) = 0 \liff a(\log_2 x - b) (\log_2 x - c) = 0 \]

som betyr at

\[ \log_2 x = b \or \log_2 x = c \]

For det første nullpunktet får vi

\[ \log_2 2 = b \liff b = 1 \]

Og for det andre nullpunktet får vi

\[ \log_2 4 = c \liff c = 2 \]

Da har vi at

\[ f(x) = a \left(\log_2 x - 1\right)(\log_2 x - 2) \]

Så ser vi at grafen går gjennom \((1, 6)\) som betyr at

\[ f(1) = 6 \liff a \cdot (\log_2 1 - 1)(\log_2 1 - 2) = 6 \]

som gir

\[ a\cdot (-1) \cdot (-2) = 6 \]
\[ 2a = 6 \liff a = 3 \]

Altså er

\[ a = 3 \and b = 1 \and c = 2 \]

Oppgave 18

2026-01-10T13:39:23.467681 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/

I figuren til høyre vises grafen til en funksjon \(f\).

Avgjør hvilken av grafene nedenfor som viser grafen til \(f'\).

2026-01-10T13:39:23.520759 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/
2026-01-10T13:39:23.573981 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/
2026-01-10T13:39:23.617434 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/
2026-01-10T13:39:23.659894 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/

Fasit

Graf C

Løsning

Grafen til \(f\) har et vendepunkt i \(x = 0\). Det betyr at den deriverte \(f'\) må ha et ekstremalpunkt der. Siden grafen til \(f\) stiger raskest der, betyr det at den deriverte må ha et toppunkt. Dette passer med graf B og C.

Vi kan se at grafen til \(f\) bare har to ekstremalpunkter, som betyr at \(f'\) bare kan ha to nullpunkter. Dette stemmer bare med graf C.

Graf C viser derfor grafen til \(f'\).

Oppgave 19

Anna jobber med en funksjon \(f\) gitt ved

\[ f(x) = -(\ln x)^2 + \ln x + 6 \]

Anna har skrevet programmet nedenfor.

 1def f(x):
 2    from math import log
 3    return -log(x)**2 + log(x) + 6
 4
 5
 6x = 0.001
 7h = 1e-6
 8while (f(x + h) - f(x)) / h > 0:
 9    x = x + 0.01
10
11print(x)

Bestem en eksakt verdi for verdien programmet skriver ut når det kjøres.

Fasit

\[ x = \sqrt{e} \]

Løsning

Programmet kjører så lenge \(f'(x) > 0\) som vi kan se fra linje 8 der det står

while (f(x + h) - f(x)) / h > 0:
    ...

der det er brukt at

\[ f'(x) \approx \dfrac{f(x + h) - f(x)}{h} \]

Programmet stopper når \(x\) blir stor nok til at \(f'(x) \leq 0\) som betyr at vi øker verdien til \(x\) frem til grafen til \(f\) ikke lenger stiger, men begynner å synke. Programmet bestemmer derfor \(x\)-koordinaten til et toppunkt. For å bestemme den eksakte verdien til verdien programmet skriver ut når det kjøres, løser vi derfor \(f'(x) = 0\). Vi deriverer først:

\[\begin{split} \begin{align*} f'(x) &= \left(-(\ln x)^2 + \ln x + 6\right)' \\ \\ &= -2 \ln x \cdot \dfrac{1}{x} + \dfrac{1}{x} + 0 \\ \\ &= \dfrac{-2 \ln x + 1}{x} \end{align*} \end{split}\]

Så løser vi likningen \(f'(x) = 0\):

\[ \dfrac{-2 \ln x + 1}{x} = 0 \liff -2 \ln x + 1 = 0 \]
\[ 2 \ln x = 1 \liff \ln x = \dfrac{1}{2} \]

som betyr at

\[ x = e^{1/2} = \sqrt{e} \]

Programmet skriver altså ut en tilnærming til \(x = \sqrt{e}\).

Oppgave 20

Nedenfor vises en grenseverdi.

Bestem grenseverdien dersom den eksisterer.

\[ \lim_{x \to -2} \dfrac{x^2 - x + 2}{x^2 - 2x - 8} \]

Fasit

\[ \lim_{x \to -2} \dfrac{x^2 - x + 2}{x^2 - 2x - 8} = \pm\infty \]

  1. Bestem \(a\) slik at grenseverdien eksisterer

\[ \lim_{x \to -2} \dfrac{x^2 + ax + 2}{x^2 - 2x - 8} \]

  1. Bestem grenseverdien for denne verdien av \(a\).

Fasit

\[ a = 3 \qog \lim_{x \to -2} \dfrac{x^2 + 3x + 2}{x^2 - 2x - 8} = \dfrac{1}{6} \]

Oppgave 21

2026-01-10T13:39:23.707941 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/

I figuren til høyre vises grafen til en funksjon \(f\).

Nedenfor vises fire figurer der én viser grafen til \(f'\) og én viser grafen til \(f''\).

Bestem hvilken figur som viser \(f'\) og hvilken som viser \(f''\).

2026-01-10T13:39:23.751999 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/
2026-01-10T13:39:23.796831 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/
2026-01-10T13:39:23.846400 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/
2026-01-10T13:39:23.895925 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/

Fasit

  • Figur A viser grafen til \(f'\)

  • Figur D viser grafen til \(f''\)

Oppgave 22

I figuren nedenfor vises kurven til en ellipse der punktene \((x, y)\) på kurven oppfyller likningen

\[ x^2 + \dfrac{y^2}{4} = 1 \]

Et rektangel med hjørner \((x, y)\), \((-x, y)\), \((x, -y)\) og \((-x, -y)\) er innskrevet i ellipsen.

Bestem \(x\) og \(y\) slik at arealet av rektangelet er størst mulig.

2026-01-10T13:39:23.941145 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/

Fasit

\[ x = \dfrac{\sqrt{2}}{2} \and y = \sqrt{2} \]

Oppgave 23

Bjørn jobber med funksjonen

\[\begin{split} f(x) = \begin{cases} \dfrac{x - 9}{\sqrt{x} - 3} & \qhvis x \neq 9 \\ \\ a & \qhvis x = 9 \end{cases} \end{split}\]

Bestem \(a\) slik at \(f\) er kontinuerlig i \(x = 9\).

Fasit

\[ a = 6 \]

Løsning

\(f\) er kontinuerlig i \(x = 9\) dersom

\[ \lim_{x \to 9} f(x) = f(9) = a \]

Vi regner ut grenseverdien:

\[\begin{split} \begin{align*} \lim_{x \to 9} f(x) &= \lim_{x \to 9} \dfrac{x - 9}{\sqrt{x} - 3} \\ \\ &= \lim_{x \to 9} \dfrac{(\sqrt{x} - 3)(\sqrt{x} + 3)}{\sqrt{x} - 3} \\ \\ &= \lim_{x \to 9} (\sqrt{x} + 3) \\ \\ &= \sqrt{9} + 3 \\ \\ &= 3 + 3 \\ \\ &= 6 \end{align*} \end{split}\]

Altså må \(a = 6\) for at \(f\) skal være kontinuerlig i \(x = 9\).

Bjørn har skrevet programmet nedenfor.

 1def f(x):
 2    if x != 9:
 3        return (x - 9) / (x**0.5 - 3)
 4    else:
 5        return a
 6
 7
 8h = 1e-6
 9x = 9
10
11dfdx = (f(x + h) - f(x)) / h
12print(dfdx)

Hva er det Bjørn prøver å regne ut med programmet?

Bestem en eksakt verdi for verdien programmet skriver ut når det kjøres med riktig verdi for \(a\).

Fasit

\[ f'(9) = \dfrac{1}{6} \]

Løsning

Programmet prøver å regne ut \(f'(9)\) som vi kan se fra linje 11 der det står

dfdx = (f(x + h) - f(x)) / h

og fra linje 8 og 9 der h = 1e-6 og x = 9 er definert. Vi kan bestemme den eksakte verdien for verdien programmet skriver ut når det kjøres ved å bruke definisjonen av den deriverte:

\[\begin{split} \begin{align*} f'(9) &= \lim_{x \to 9} \dfrac{f(x) - f(9)}{x - 9} \\ \\ &= \lim_{x \to 9} \dfrac{\dfrac{x - 9}{\sqrt{x} - 3} - 6}{x - 9} \\ \\ &= \lim_{x \to 9} \dfrac{\dfrac{x - 9 - 6(\sqrt{x} - 3)}{\sqrt{x} - 3}}{x - 9} \\ \\ &= \lim_{x \to 9} \dfrac{x - 9 - 6\sqrt{x} + 18}{(x - 9)(\sqrt{x} - 3)} \\ \\ &= \lim_{x \to 9} \dfrac{x - 6\sqrt{x} + 9}{(x - 9)(\sqrt{x} - 3)} \\ \\ &= \lim_{x \to 9} \dfrac{(\sqrt{x} - 3)^2}{(x - 9)(\sqrt{x} - 3)} \\ \\ &= \lim_{x \to 9} \dfrac{\sqrt{x} - 3}{x - 9} \\ \\ &= \lim_{x \to 9} \dfrac{\sqrt{x} - 3}{(\sqrt{x} - 3)(\sqrt{x} + 3)} \\ \\ &= \lim_{x \to 9} \dfrac{1}{\sqrt{x} + 3} \\ \\ &= \dfrac{1}{\sqrt{9} + 3} \\ \\ &= \dfrac{1}{3 + 3} \\ \\ &= \dfrac{1}{6} \end{align*} \end{split}\]

Altså skriver programmet ut en tilnærming til

\[ f'(9) = \dfrac{1}{6} \]

Oppgave 24

Ifølge Newtons avkjølingslov vil temperaturen \(T\) til et objekt etter \(t\) minutter være

\[ \ln (T - T_0) = -k\cdot t + r \]

hvor \(T_0\) er romtemperaturen, og \(k\) og \(r\) er konstanter.

I et rom med temperatur \(22 \degree \mathrm{C}\) setter vi en kopp med kaffe. Ved tidspunktet \(t = 0\) er temperaturen i kaffen \(96 \degree \mathrm{C}\), og etter 10 minutter er temperaturen \(70 \degree \mathrm{C}\).

Vis at

\[ T(t) = T_0 + e^{-kt + r} \]

Bestem \(T_0\), \(k\) og \(r\).

Fasit

\[ T_0 = 22 \and k = -\dfrac{3 \ln 2 + \ln 3 - \ln 37}{10} \and r = \ln 2 + \ln 37 \]

Hvor lang tid vil det ta før temperaturen i kaffen er mindre enn \(30 \degree \mathrm{C}\)?

Fasit

ca. 51 minutter.

Når vil temperaturen synke med \(1 \, \degree \mathrm{C}\) per minutt?

Fasit

Etter ca. 27 minutter.

Oppgave 25

2026-01-10T13:39:23.989672 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/

Anna jobber med en oppgave om en funksjon \(f\) og har laget seg figuren som er vist til høyre. Funksjonen \(f\) er gitt ved

\[ f(x) = (x^2 - 9)^4 \qfor x \in \langle 0, 3 \rangle \]

Anna har skrevet programmet nedenfor.

 1def A(x):
 2    return x * (x**2 - 9) ** 4
 3
 4
 5t = 0
 6dt = 0.01
 7
 8while A(t) < A(t + dt):
 9    t = t + dt
10
11print(t)

  1. Forklar hva Anna prøver å finne ut med programmet.

  2. Bestem en eksakt verdi for verdien programmet skriver ut når det kjøres.

Fasit

  1. Anna prøver å bestemme hvilken verdi for \(t\) som gir størst evrdi for arealet av rektangelet.

  2. Den eksakte verdien for \(t\) som gir størst areal er \(t = 1\).

Oppgave 26

En funksjon \(f\) er gitt ved

\[\begin{split} f(x) = \begin{cases} 2x^2 + 3x + a & \qhvis x < 1 \\ \\ -2x^2 + bx & \qhvis x \geq 1 \end{cases} \end{split}\]

Bestem \(a\) og \(b\) slik at \(f\) er deriverbar i \(x = 1\)

Fasit

\[ a = 4 \and b = 11 \]

Oppgave 27

2026-01-27T12:52:45.925349 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/

I figuren til høyre vises grafen til

\[ f(x) = e^{-x^2} \]

og et rektangel som er innskrevet under grafen.

Bestem det største mulige arealet et slikt rektangel kan ha.

Fasit

\[ \sqrt{\dfrac{2}{e}} \]

Oppgave 28

En funksjon \(f\) er gitt ved

\[\begin{split} f(x) = \begin{cases} a(x - 2)^2 + b &\qhvis x < 0 \\ \\ cx + 1 &\qhvis 0 \leq x < 2 \\ \\ -x^3 + dx^2 + 1 &\qhvis x \geq 2 \end{cases} \end{split}\]

Bestem \(a\), \(b\), \(c\) og \(k\) slik at \(f\) er deriverbar i \(x = 0\) og \(x = 2\).

Fasit

\[ a = -1 \and b = 5 \and c = 4 \and d = 4 \]

Oppgave 29

2026-01-10T13:39:24.098802 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/

Grafen til en funksjon \(f\) er vist i figuren til høyre.

Nedenfor vises fire alternativer med mulige egenskaper for grafen til \(f'\).

Kun ett alternativ stemmer – hvilket?






Alternativ 1

\[\begin{split} \begin{align*} \lim_{x \to -1^-} f'(x) &= \infty \\ \\ \lim_{x\to -1^+} f'(x) &= -\infty \\ \\ \lim_{x \to -\infty} f'(x) &= 3 \end{align*} \end{split}\]

Alternativ 2

\[\begin{split} \begin{align*} \lim_{x \to -1^-} f'(x) &= -\infty \\ \\ \lim_{x\to -1^+} f'(x) &= -\infty \\ \\ \lim_{x \to \infty} f'(x) &= -3 \end{align*} \end{split}\]

Alternativ 3

\[\begin{split} \begin{align*} \lim_{x \to -1^-} f'(x) &= \infty \\ \\ \lim_{x\to -1^+} f'(x) &= \infty \\ \\ \lim_{x \to -\infty} f'(x) &= 3 \end{align*} \end{split}\]

Alternativ 4

\[\begin{split} \begin{align*} \lim_{x \to -1^-} f'(x) &= \infty \\ \\ \lim_{x\to -1^+} f'(x) &= \infty \\ \\ \lim_{x \to \infty} f'(x) &= -3 \end{align*} \end{split}\]

Fasit

Alternativ 3

Oppgave 30

2026-01-10T13:39:24.143482 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/

Grafen til \(f'\) er vist i figuren til høyre.

Nedenfor vises fire grafer der én viser grafen til \(f\) og én viser grafen til \(f''\).

Bestem hvilken graf som viser \(f\) og hvilken som viser \(f''\).

2026-01-10T13:39:24.188189 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/
2026-01-10T13:39:24.228346 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/
2026-01-10T13:39:24.268160 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/
2026-01-10T13:39:24.307570 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/

Fasit

  • Figur A viser grafen til \(f\)

  • Figur B viser grafen til \(f''\)

Oppgave 31

En funksjon \(f\) er gitt ved

\[\begin{split} f(x) = \begin{cases} \sqrt{x + a} &\qhvis -a < x < 0 \\ \\ x^2 + bx + 4 &\qhvis x \geq 0 \end{cases} \end{split}\]

Bestem \(a\) og \(b\) slik at \(f\) er deriverbar i \(x = 0\).

Fasit

\[ a = 16 \and b = \dfrac{1}{8} \]

Oppgave 32

En funksjon \(f\) er gitt ved

\[ f(x) = 6x - x^2 \qfor x \in [0, 6] \]

Nedenfor vises grafen til \(f\) sammen med et rektangel \(ABCD\).

I rektangelet er \(A(a, 0)\) og \(D(a, f(a))\) der \(a \in \langle 0, 3\rangle\). Punktet \(C\) ligger på grafen til \(f\).

Bestem \(a\) slik at arealet av rektangelet \(ABCD\) er størst mulig.

2026-01-10T13:39:24.353713 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/

Fasit

\[ a = -\sqrt{3} + 3 \]

Oppgave 33

En funksjon \(f\) er gitt ved

\[\begin{split} f(x) = \begin{cases} 2x^2 - 3x - 2 &\qhvis x \leq a \\ \\ x^2 + x + 3 &\qhvis x > a \end{cases} \end{split}\]

For hvilke verdier av \(a\) er \(f\) kontinuerlig?

Fasit

\[ a = -1 \or a = 5 \]

Undersøk om \(f\) er deriverbar i \(x = a\) for verdiene av \(a\) du fant.

Fasit

\(f\) er ikke deriverbar for verdiene noen av verdiene.

Oppgave 34

Fire byer \(A\), \(B\), \(C\) og \(D\) ligger plassert slik at de danner et kvadrat med sidelengde \(10\) km.

Vi skal lage en veiforbindelse mellom disse fire byene. Veilengden mellom de fire byene blir kortest mulig dersom vi lager veiene via to punkter \(E\) og \(F\). Se figuren nedenfor.

Vi lar \(x\) være avstanden mellom \(E\) og \(F\).

Bestem \(x\) slik at den samlede veilengden mellom byene blir kortest mulig.

2026-01-10T13:39:24.392072 image/svg+xml Matplotlib v3.9.1, https://matplotlib.org/

Fasit

\[ x = \dfrac{-10\sqrt{3} + 30}{3} \]