5. Numerisk løsning av likninger#
Halveringsmetoden#
Halveringsmetoden er en strategi for å systematisk løse likninger. Ideen er som følger:
Halveringsmetoden
For en funksjon \(f\), kan vi finne et nullpunkt \(x\) slik at \(f(x) = 0\) ved å bruke følgende strategi:
Velg et intervall \([a, b]\) slik at \(f(a)\) og \(f(b)\) har motsatte fortegn.
Beregn midtpunktet \(c = \dfrac{a + b}{2}\) på intervallet.
Sjekk fortegnet til \(f(c)\):
Hvis \(f(c) = 0\), har vi funnet nullpunktet.
Hvis \(f(c)\) har samme fortegn som \(f(a)\), sett det nye intervallet til \([c, b]\).
Hvis \(f(c)\) har samme fortegn som \(f(b)\), sett det nye intervallet til \([a, c]\).
Gjenta dette frem til \(f(c) \approx 0\) (det vil si at \(f(c)\) er tilstrekkelig nærme null). Da er \(x = c\) nullpunktet til \(f\).
Se animasjonen nedenfor.
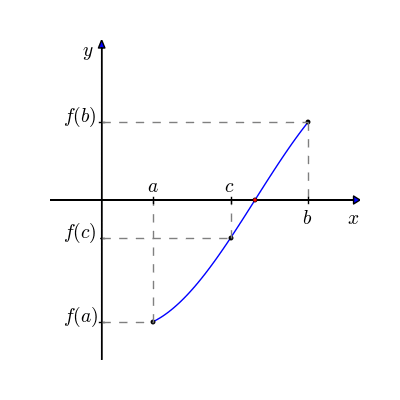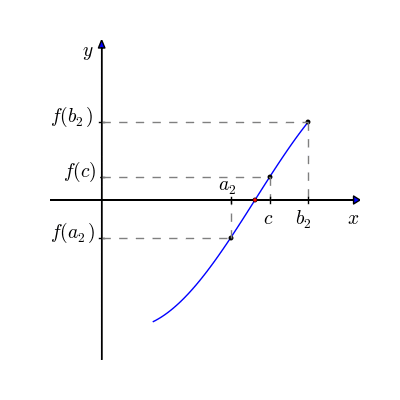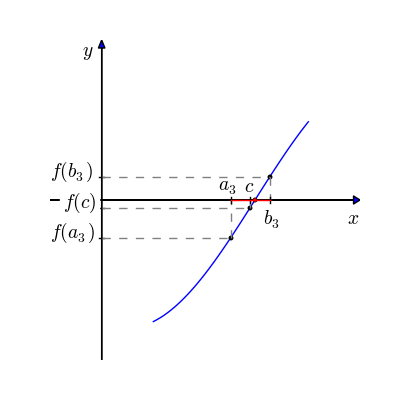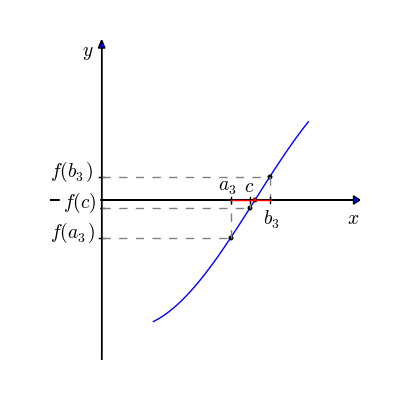
Fig. 5.1 Animasjonen starter med intervallet \([a_1, b_1]\) og regner ut et midtpunkt \(c\). Deretter velges det intervallet hvor funksjonen skifter fortegn, og prosessen gjentas. Etter hvert nærmer \(c\) seg verdien til nullpunktet.#
Halveringsmetoden (Bisection method) laget av Picknick, lisensiert under CC BY-SA 4.0 via Wikimedia Commons.
Oppgave 1
Programmet nedenfor bruker halveringsmetoden, men er plassert i tilfeldig rekkefølge.
Sett programmet i riktig rekkefølge.
Kjør programmet nedenfor og gi en tolkning av det programmet skriver ut.
I programmet nedenfor ser du noen kommentarer merket # ????.
Bytt ut ???? og forklar hva programmet gjør med korte kommentarer.
Hvilken betydning har a og b i programmet?
Hva skjer hvis f(a) og f(b) har samme fortegn? Prøv med i programmet.
Hvilken betydning har nøyaktighet i programmet?
Prøv forskjellige verdier og trekk en konklusjon.
Modifiser programmet og prøv følgende
Velg en annen funksjon \(f(x)\).
La brukeren skriv inn verdiene til
aogbmedinput()-funksjonen.Skriv en mer informativ melding som skrives ut når programmet har løst likningen.
Skriv en informativ melding som forteller når intervallet \([a, b]\) ikke inneholder et nullpunkt.
